Question

If the graph of the expression $y = {x^2} - 8x + 12$ is shown in the figure. Then area of the square ABCD inscribed between parabola and $x$-axis is given by

(a) $12 + 4\sqrt 5$
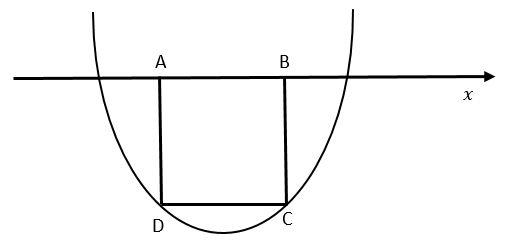
(b) $12 - 4\sqrt 5$
(c) $24 + 8\sqrt 5$
(d) $24 - 8\sqrt 5$

Answer 1

Hint:** To find the area of the square, we need to find the length of one side of the square. The best way to do that would be to convert the given equation into the equation of parabola. And then using that equation we will try to find the coordinates of C to get the length of the side of the given square.

Complete step by step solution:
Let us first convert the given equation into the equation of parabola.
$y = {x^2} - 8x + 12$
Rearranging the above equation, we get
$y = {x^2} - 2 \times 4x + 16 - 4$
$\Rightarrow y = {(x - 4)^2} - 4$
$\Rightarrow y + 4 = {(x - 4)^2}$ . . . (1)
We know that, $y - k = 4a{(x - h)^2}$represents a parabola with vertex at (h, k). Using this concept, we can conclude that the quadratic equation we simplified is a parabola with vertex at V (4, -4).
From the figure, you can observe that the coordinates of W will be W (4, 0).
Let us assume that the distance between W and B is $a.$Then the coordinates of B will be B (4+a, 0).
We know that parabola is symmetric. So if $WB = a$then $AB = 2a$
Since, ABCD is a square, $BC = 2a$
Therefore, the coordinates of C will be C (4+a, -2a)

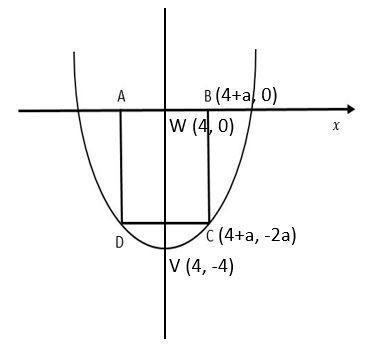
Since, C lies on the parabola, the coordinates of C must satisfy equation (1)
$\therefore y + 4 = {(x - 4)^2}$
$\Rightarrow - 2a + 4 = {(4 + a - 4)^2}$
$\Rightarrow - 2a + 4 = {a^2}$
Rearranging the above equation, we get
${a^2} + 2a - 4 = 0$
By using the quadratic formula, $x = \dfrac{{ - b \pm \sqrt {{b^2} - 4ac} }}{{2a}}$, we get
$\Rightarrow a = \dfrac{{ - 2 \pm \sqrt {4 + 4 \times 4} }}{2}$
$\Rightarrow a = - 1 \pm \sqrt {1 + 4}$
$\Rightarrow a = - 1 \pm \sqrt 5$
$a = - 1 - \sqrt 5$is a negative value. But we have taken $a$as a distance. Therefore $a$cannot take this value.
Hence, $a = - 1 + \sqrt 5$
Thus, length of one side of a square is $2a = - 2 + 2\sqrt 5$
Hence, the area of the square is ${(2a)^2} = {( - 2 + 2\sqrt 5 )^2}$
$= 4 \times 5 + 4 - 8\sqrt 5$ (Using, ${(a - b)^2} = {a^2} + {b^2} - 2ab$)
$= 20 + 4 - 8\sqrt 5$
$= 24 - 8\sqrt 5$
Hence the answer is (d) $= 24 - 8\sqrt 5$

Note: Such questions cannot be solved using only what is given in the question. You need to figure out additional points to solve the problem using the given information. This question can only be solved if you know the graph and properties of parabola.