Question

If the function $\frac{2\pi}{3}$ is continuous in the interval $\left( \frac{x - 2}{2} \right)$ then the values of a and b are respectively

• A. 0, 2
• B. 1, 1
• C. 2, 0
• D. 2, 1

Answer 1

Answer: (C)

2, 0

Answer 2

$\bullet \bullet$ The turning points for $f ( x )$ are

So, $\lim _ { x \rightarrow 1 ^ { - } } f ( x ) = \lim _ { h \rightarrow 0 } f ( 1 - h )$ = $\lim _ { h \rightarrow 0 } \left[ 1 + \sin \frac { \pi } { 2 } ( 1 - h ) \right]$

=$\left[ 1 + \sin \left( \frac { \pi } { 2 } - 0 \right) \right]$ = 2

Similarly, $\lim _ { x \rightarrow 1 ^ { + } } f ( x ) = \lim _ { h \rightarrow 0 } f ( 1 + h )$ = $\lim _ { h \rightarrow 0 } a ( 1 + h ) + b$ = a + b

$\bullet \bullet$ $f ( x )$ is continuous at so $\lim _ { x \rightarrow 1 ^ { - } } f ( x ) = \lim _ { x \rightarrow 1 ^ { + } } f ( x ) = f ( 1 )$

⇒ $2 = a + b$ ..…..(i)

Again, $\lim _ { x \rightarrow 3 ^ { - } } f ( x ) = \lim _ { h \rightarrow 0 } f ( 3 - h )$ = $\lim _ { h \rightarrow 0 } a ( 3 - h ) + b$ = $3 a + b$

and $\lim _ { x \rightarrow 3 ^ { + } } f ( x ) = \lim _ { h \rightarrow 0 } f ( 3 + h )$ = $\lim _ { h \rightarrow 0 } 6 \tan \frac { \pi } { 12 } ( 3 + h )$ = 6

$f ( x )$ is continuous in $( - \infty , 6 )$, so it is continuous at $x = 3$ also, so $\lim _ { x \rightarrow 3 ^ { - } } f ( x ) = \lim _ { x \rightarrow 3 ^ { + } } f ( x ) = f ( 3 )$

⇒ $3 a + b = 6$ .….(ii)

Solving (i) and (ii) a = 2, b = 0.

Trick : In above type of questions first find out the turning points. For example in above question they are x = 1,3. Now find out the values of the function at these points and if they are same then the function is continuous i.e., in above problem.

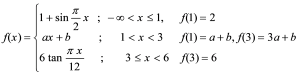
Which gives $2 = a + b$ and $6 = 3 a + b$ after solving above linear equations we get $a = 2 , b = 0$ .