Question

If the function f(x) satisfies $f\left( {\dfrac{{x + 2y}}{3}} \right) = \dfrac{{f(x) + 2f(y)}}{3},\forall x,y \in R$ and ${f^1}(0) = 1$ then show that $f(x)$ is continuous for all $x \in R$.

Answer 1

To prove that $f(x)$ is continuous for all $x \in R$ first of all we have to draw coordinate axis as shown in the diagram given below,

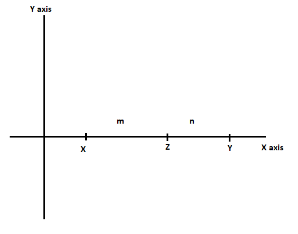
In the figure given above the horizontal line is the x-axis and vertical line is y-axis. Now, we have to let two points (x, y) in the x-axis so that we can find that the given function is line, circle or parabola e.t.c. and let that a point z divides the points in the ration (m : n) as shown in the diagram given below.

Now, we will obtain the value of point above the point z to check if the function is linear or not and is continuous or not for all $x \in R$.

Complete step-by-step answer:
Given,
$f\left( {\dfrac{{x + 2y}}{3}} \right) = \dfrac{{f(x) + 2f(y)}}{3},\forall x,y \in R$
And ${f^1}(0) = 1$
Step 1: First of all we have to draw the coordinate axis according to the diagram given below

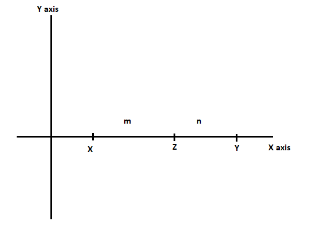
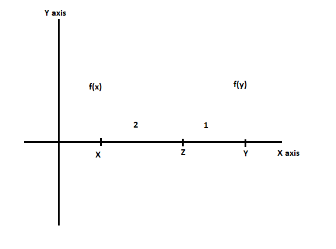
The horizontal line is x-axis and vertical line is y-axis and let x and y are two points on the x-axis and the point z is between the points x and y axis which divides them in the ratio (2 : 1) we can also understand it with the help of the diagram given below,

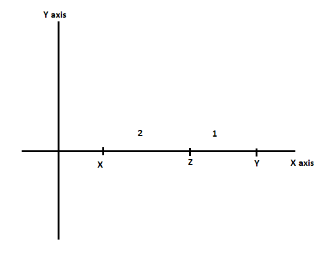
Step 2: Now, we will find the coordinates of point z with the help of the formula (1) as mentioned in the solution hint. On substituting all the values,
$z = \dfrac{{2y + x}}{{2 + 1}} \\\ z = \dfrac{{x + 2y}}{3} \\\$
Step 3: Here, as we know the value of point above point x will be $f(x)$ and value of point above point y will be $f(y)$. We can also understand it with the help of the diagram given below,

Step 4: Now, according to the question $f\left( {\dfrac{{x + 2y}}{3}} \right) = \dfrac{{f(x) + 2f(y)}}{3},\forall x,y \in R$ on joining the point $f(x)$ and $f(y)$ the value of point above z will be $\dfrac{{f(x) + 2f(y)}}{3}$ we can also understand it with the help of the diagram given below.

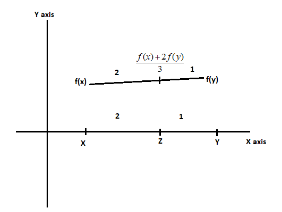
Step 5: Hence, we can clearly say that our function is linearly increasing and linearly decreasing. So, our function$f(x)$ is a linear function.
Step 6: Now, we can write our function in the form of linear equation as,
$f(x) = mx + c$
So, we can say that $f(x)$is continuous for all $x \in R$.
As, from the above step by step solution we obtained that $f(x)$ is a linear equation hence, we can say that $f(x)$ is continuous for all $x \in R$.

Note: A function is said to be a continuous function if it is continuous at every point in it’s domain.
To become aware of problems of determining whether the given function is continuous by using graphical techniques.
If the obtained function is in the form of a line then we can say that given function is continuous.