Question

If the foot of the perpendicular from the origin to a straight line is at the point $(3, - 4)$. Then, the equation of the line is
1. $3x - 4y = 25$
2. $3x - 4y + 25 = 0$
3. $4x + 3y - 25 = 0$
4. $4x + 3y + 25 = 0$

Answer 1

We are given the foot of the perpendicular from origin and we have to find the equation of line. To find this we will find the slope of the tangent of line from origin to the given point. Then find the slope of the normal line from the origin to the given point. Find the equation of required line using the slope and one point form.

Complete step-by-step solution:
The slope or gradient of a line is a number that describes both the direction and the steepness of the line. Slope is often denoted by the letter m.
A line is increasing if it goes up from left to right. The slope is positive, i.e. $m > 0$.
A line is decreasing if it goes down from left to right. The slope is negative, i.e. $m < 0$.
If a line is horizontal the slope is zero. This is a constant function.
If a line is vertical the slope is undefined .
The slope of line passing through the origin and the point $(3, - 4)$ is $\dfrac{{ - 4 - 0}}{{3 - 0}} = - \dfrac{4}{3}$
The slope of normal to this line $= \dfrac{3}{4}$
Now equation of line with slope $= \dfrac{3}{4}$and passing through $(3, - 4)$ is
$y + 4 = \dfrac{3}{4}(x - 3)$
On cross multiplication and simplification we get ,
$4\left( {y + 4} \right) = 3(x - 3)$
On simplifying the above equation we get ,
$3x - 4y = 25$

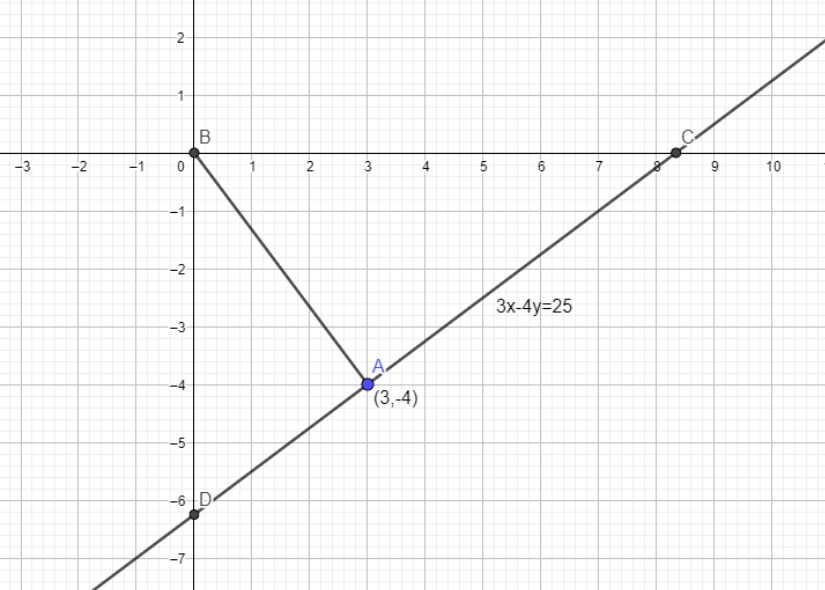
Hence we get the required equation of line.
Therefore, option (1) is the correct answer.

Note: In order to solve such types of questions one must know about slope and how to find it.Find the slope of the line using appropriate formula. The steepness, incline, or grade of a line is measured by the absolute value of the slope. A slope with a greater absolute value indicates a steeper line. Do the calculations very carefully and recheck them so that the answer may not get altered.