Question

If the first point of trisection of AB is (t, 2t) and the ends A, B move on ‘x’ and ‘y’ axis respectfully, then the focus of midpoint of AB is
A.x = y
B.2x = y
C.4x = y
D.x = 4y

Answer 1

Hint : We know the section formula, the coordinates of the point P(x, y) which divides the line segment joining the points $A({x_1},{y_1})$ and $B({x_2},{y_2})$ internally, in the ratio ${m_1}:{m_2}$ are $\left( {\dfrac{{{m_1}{x_2} + {m_2}{x_1}}}{{{m_1} + {m_2}}},\dfrac{{{m_1}{y_2} + {m_2}{y_1}}}{{{m_1} + {m_2}}}} \right)$ . We choose the midpoint as $M(h,k)$ and using the above formula we find the coordinate values ‘h’ and ‘k’ to obtain the required result.

Complete step-by-step answer :
Let $M(h,k)$ be the midpoint of line AB. Given A, B move on the ‘x’ and ‘y’ axis respectively. Then it is obvious that the coordinates of A and B are $A(2h,0)$ and $B(0,2k)$ .
Since point $P(t,2t)$ is first trisection it divides A and B into $1:2$ ratio. See in the below diagram for understanding point of view.

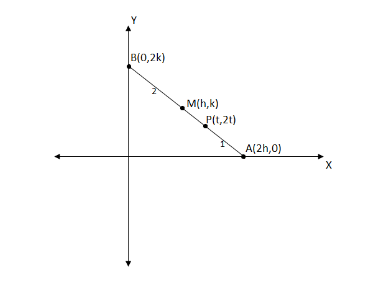
We have $A({x_1},{y_1}) = A(2h,0)$ , $B({x_2},{y_2}) = B(0,2k)$ and which divides in the ratio $1:2$ . Using the section formula we find the coordinates of the point P.
Using the formula $\left( {\dfrac{{{m_1}{x_2} + {m_2}{x_1}}}{{{m_1} + {m_2}}},\dfrac{{{m_1}{y_2} + {m_2}{y_1}}}{{{m_1} + {m_2}}}} \right)$
$\Rightarrow = P\left( {\dfrac{{\left( {1 \times 0} \right) + \left( {2 \times 2h} \right)}}{{1 + 2}},\dfrac{{\left( {1 \times 2k} \right) + \left( {2 \times 0} \right)}}{{1 + 2}}} \right)$
$\Rightarrow = P\left( {\dfrac{{0 + 4h}}{3},\dfrac{{2k + 0}}{3}} \right)$
$\Rightarrow = P\left( {\dfrac{{4h}}{3},\dfrac{{2k}}{3}} \right)$
But we already have point p coordinates as $P(t,2t)$ .
Comparing ‘x’ and ‘y’ coordinates in both Points P we have
The ‘x’ coordinate $\dfrac{{4h}}{3} = t$
Multiply by 3 on both sides.
$\Rightarrow 4h = 3t{\text{ - - - - - - - (1)}}$
The ‘y’ coordinate $\dfrac{{2k}}{3} = 2t$
Cancelling 2 on both sides,
$\Rightarrow \dfrac{k}{3} = t$
Multiply by 3 on both sides,
$\Rightarrow k = 3t{\text{ - - - - - - - (2)}}$
Now substituting equation (2) in equation (1) we have $\Rightarrow 4h = k$ .
But we have options in ‘x’ and ‘y’ variables, so we have
$\Rightarrow 4x = y$ (Because $(h,y) = (x,y)$ )
So, the correct answer is “Option C”.

Note : In general Trisection is the division of a quantity or figure into three equal parts. In the above problem when P is the first trisection there is another two trisection. Hence we take the ratio as $1:2$ . Remember the formula of section formula. Careful in the substitution and calculation part.