Question

If the first point of trisection of AB is $\left( {t,2t} \right)$ and the ends A, B moves on x and y axis respectively, then locus of midpoint of AB is
A.$x = y$
B.$2x = y$
C.$4x = y$
D.$x = 4y$

Answer 1

Here, we will divide a line segment into three parts. Then by using the section formula and the given co-ordinates we will find the coordinates of the line segment. Then by equating the co-ordinates of P, we will find the locus of midpoint of AB.

Formula Used:
Section formula: $\left( {\dfrac{{m{x_2} + n{x_1}}}{{m + n}},\dfrac{{m{y_2} + n{y_1}}}{{m + n}}} \right)$ where $m:n$ is the ratio of a point dividing the line segment and $\left( {{x_1},{y_1}} \right)$ , $\left( {{x_2},{y_2}} \right)$ are the coordinates of the line segment.

Complete step-by-step answer:
We will first draw the diagram based on the given information.

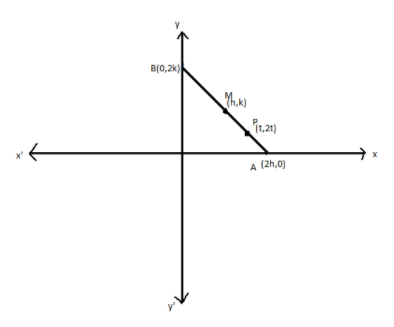
Let P and M be the points of Trisection of the line segment joining the points A$\left( {2h,0} \right)$ and B$\left( {0,2k} \right)$ such that P is nearer to A. Let P$\left( {t,2t} \right)$ and M$\left( {h,k} \right)$ be the co-ordinates of the points P and M.
Therefore, P divides the line segment in the ratio $1:2$ and Q divides the line segment in the ratio $2:1$.
By using the section formula $\left( {\dfrac{{m{x_2} + n{x_1}}}{{m + n}},\dfrac{{m{y_2} + n{y_1}}}{{m + n}}} \right)$, we get
$\Rightarrow$ Co-ordinates of P$= \left( {\dfrac{{1\left( 0 \right) + 2\left( {2h} \right)}}{{1 + 2}},\dfrac{{1\left( {2k} \right) + 2\left( 0 \right)}}{{1 + 2}}} \right)$
Multiplying the terms, we get
$\Rightarrow \left( {t,2t} \right) = \left( {\dfrac{{4h}}{3},\dfrac{{2k}}{3}} \right)$
$\Rightarrow \left( {\dfrac{{4h}}{3},\dfrac{{2k}}{3}} \right) = \left( {t,2t} \right)$
By comparing the co-ordinates of $x$ and $y$, we get
$\Rightarrow \dfrac{{4h}}{3} = t$ and $\dfrac{{2k}}{3} = 2t$
$\Rightarrow 4h = 3t$ and $2k = 6t$
$\Rightarrow 4h = 3t$ and $k = 3t$
By substituting $k = 3t$ in $4h = 3t$, we get
$4h = k$
So, by substituting the co-ordinates, we get
$\Rightarrow 4x = y$
Therefore, the locus of midpoint of AB is $4x = y$ and thus Option (C) is the correct answer.

Note: We know that trisection is the division of a line segment into three equal parts. Section formula is used to determine the co-ordinate of a point that divides a line segment joining two points into two parts such that their ratio of length is $m:n$. The sectional formula can also be used to find the co-ordinate of a point that lies outside a circle.