Question

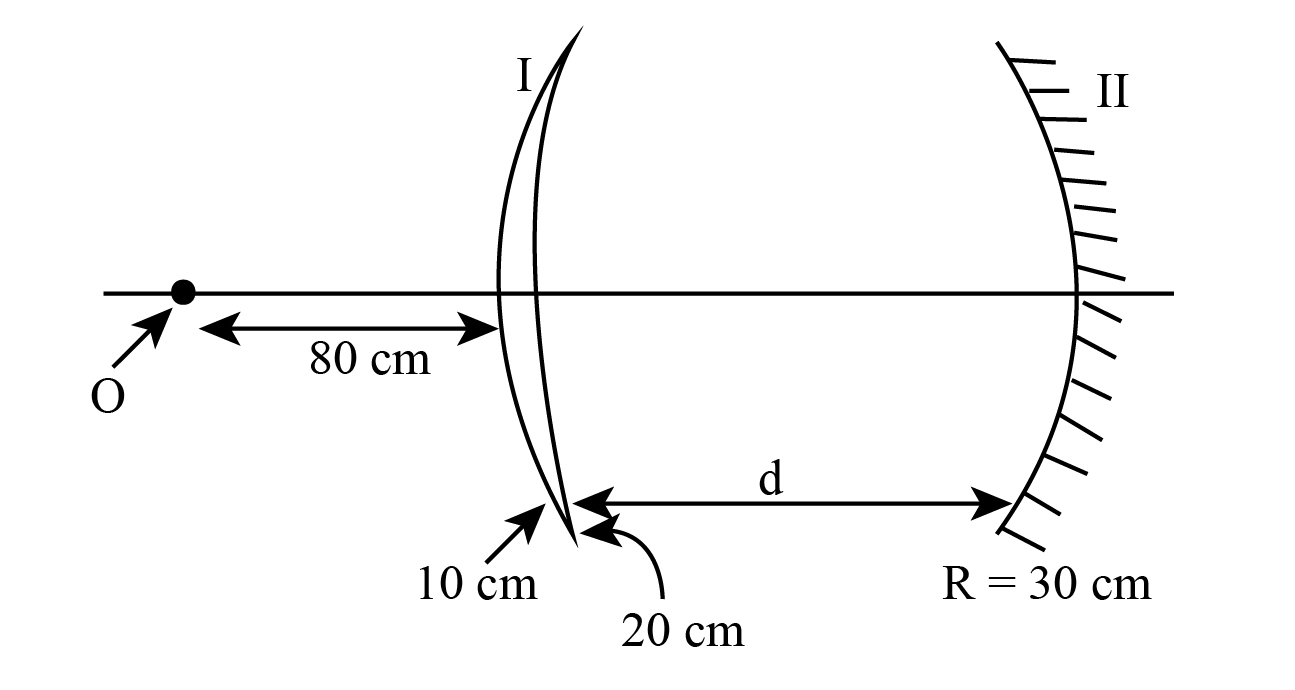
If the final image formed after two reflections through the lens and one reflection from the mirror forming at the same point 'O' then find the value of d. (if $\mu$ is refractive index of material of lens is 1.5)

A. $100\;{\rm{cm}}$
B. $110\;{\rm{cm}}$
C. $90\;{\rm{cm}}$

Answer 1

The above problem can be resolved using the concept and fundamentals of the location of the image after being reflected by the eye lens. The relation for the distance between the curvature of the lens and the front part of the lens is given by taking the sum of twice the focal length and the radius of curvature. To find the focal length, the formula for the focal length in terms of the refractive index of the lens can be used.

Complete step by step answer:
Given:
The refractive index of the material of the lens is, $\mu = 1.5$.
From the given figure, the radius of curvature of the lens is, $R = 30\;{\rm{cm}}$
And the inner and outer radii are ${R_1}$ and ${R_2}$, and their values are 10 cm and 20 cm respectively.
Then, the focal length of lens is,

f = \left( {\mu - 1} \right)\left( {\dfrac{1}{{{R_1}}} - \dfrac{1}{{{R_2}}}} \right)\\\ f = \left( {1.5 - 1} \right)\left( {\dfrac{1}{{10\;{\rm{cm}}}} - \dfrac{1}{{20\;{\rm{cm}}}}} \right)\\\ f = 40\;{\rm{cm}} \end{array}$$ Then, the value of d is, $$\begin{array}{l} d = 2f + R\\\ d = 2 \times 40\;{\rm{cm}} + 30\;{\rm{cm}}\\\ d = 110\;{\rm{cm}} \end{array}$$ Therefore, the required value of d is 110 cm **So, the correct answer is “Option B”.** **Note:** In order to solve the given problem, it is necessary to understand the basic relation between the focal length and the refractive index along with the radius of curvature of the lens. Moreover, the refractive index of any medium determines the extent to which the bending of light takes place while entering from one medium to another. Besides, the fundamentals of the focal length is also considered important to resolve problems of similar kind.