Question
Question: If the expression $x(e^x-1)(x-1)(x-2)^3(x-3)^5 \ge 0$ then the true solution set is...
If the expression x(ex−1)(x−1)(x−2)3(x−3)5≥0 then the true solution set is
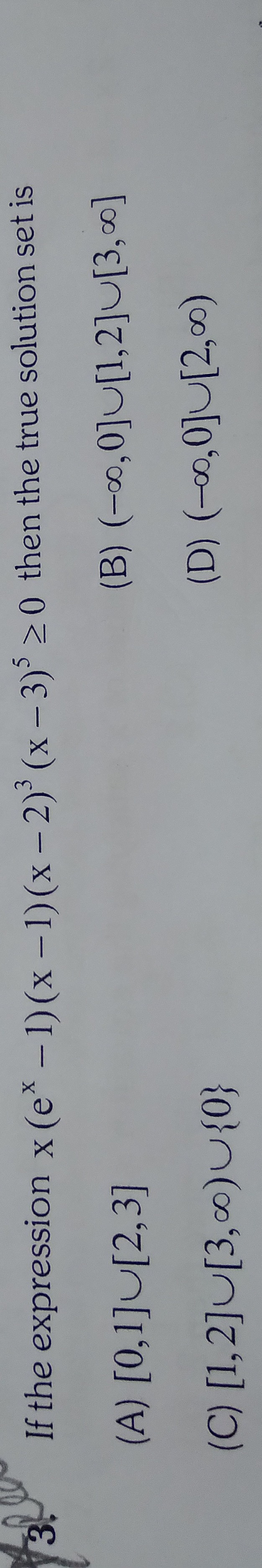
[0,1][2,3]
(-∞,0][1,2][3,∞]
[1,2][3,∞)∪{0}
(-∞,0][2,∞)
[1,2][3,∞)∪{0}
Solution
The inequality to solve is x(ex−1)(x−1)(x−2)3(x−3)5≥0.
1. Identify Critical Points: The critical points are the values of x where any of the factors become zero.
- x=0
- ex−1=0⟹ex=1⟹x=0
- x−1=0⟹x=1
- x−2=0⟹x=2
- x−3=0⟹x=3
The distinct critical points are 0,1,2,3. These points divide the number line into intervals: (−∞,0), (0,1), (1,2), (2,3), (3,∞).
2. Analyze the Sign of Each Factor: Let f(x)=x(ex−1)(x−1)(x−2)3(x−3)5. We need to determine the sign of f(x) in each interval.
- Factor x: Positive for x>0, negative for x<0.
- Factor ex−1: Positive for x>0, negative for x<0. At x=0, ex−1=0.
- Factor x−1: Positive for x>1, negative for x<1.
- Factor (x−2)3: The sign is determined by (x−2). Positive for x>2, negative for x<2.
- Factor (x−3)5: The sign is determined by (x−3). Positive for x>3, negative for x<3.
3. Sign Analysis in Intervals:
-
Interval (−∞,0):
- x: -
- ex−1: - (since x<0⟹ex<1)
- x−1: -
- (x−2)3: -
- (x−3)5: -
- f(x)=(−)×(−)×(−)×(−)×(−)=(−). So f(x)<0.
-
Interval (0,1):
- x: +
- ex−1: + (since x>0⟹ex>1)
- x−1: -
- (x−2)3: -
- (x−3)5: -
- f(x)=(+)×(+)×(−)×(−)×(−)=(−). So f(x)<0.
-
Interval (1,2):
- x: +
- ex−1: +
- x−1: +
- (x−2)3: -
- (x−3)5: -
- f(x)=(+)×(+)×(+)×(−)×(−)=(+). So f(x)>0.
-
Interval (2,3):
- x: +
- ex−1: +
- x−1: +
- (x−2)3: + (since x>2)
- (x−3)5: -
- f(x)=(+)×(+)×(+)×(+)×(−)=(−). So f(x)<0.
-
Interval (3,∞):
- x: +
- ex−1: +
- x−1: +
- (x−2)3: +
- (x−3)5: + (since x>3)
- f(x)=(+)×(+)×(+)×(+)×(+)=(+). So f(x)>0.
4. Include Critical Points: The inequality is f(x)≥0. This means we include the intervals where f(x)>0 and the points where f(x)=0. The points where f(x)=0 are 0,1,2,3.
5. Combine Results: From the sign analysis, f(x)>0 for x∈(1,2) and x∈(3,∞). Including the roots where f(x)=0: The solution set is {0}∪[1,2]∪[3,∞).
6. Match with Options: The solution set {0}∪[1,2]∪[3,∞) matches option (C).
