Question

If the equation of base of an equilateral triangle is 2x-y = 1 and the coordinates of the vertex are (-1,2), then the length of the sides of the equilateral triangle is
[a] $\sqrt{\dfrac{20}{3}}$
[b] $\dfrac{2}{\sqrt{15}}$
[c] $\sqrt{\dfrac{8}{15}}$
[d] $\sqrt{\dfrac{15}{2}}$

Answer 1

Hint: Use the fact that if a is the length of a side of an equilateral triangle, then the area of the triangle is given by $\dfrac{\sqrt{3}}{4}{{a}^{2}}$. Determine the height of the equilateral triangle by finding the distance between the point $\left( -1,2 \right)$ from the line $2x-y=1$. Assume the length of the side of the equilateral triangle be a. Hence find the area of the triangle using the formula area of a triangle $=\dfrac{1}{2}base\times height$. Equate this area to $\dfrac{\sqrt{3}}{4}{{a}^{2}}$. Hence form a linear equation in a. Solve for a. The value of a gives the length of the side of the equilateral triangle.

Complete step-by-step answer:
Let the side of the equilateral triangle be a.
We know that the distance of the point $P\left( {{x}_{1}},{{y}_{1}} \right)$ from the line $Ax+By+C=0$ is given by
$\dfrac{\left| A{{x}_{1}}+B{{y}_{1}}+C \right|}{\sqrt{{{A}^{2}}+{{B}^{2}}}}$

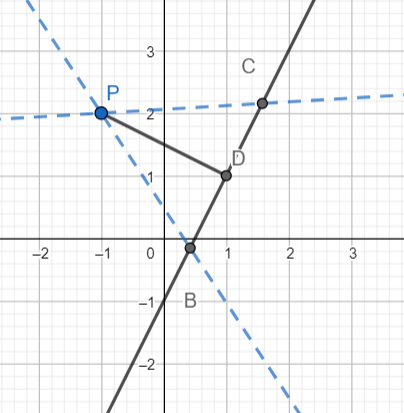
In the diagram above PBC is the required equilateral triangle.
Hence the distance of point P(-1,2) from 2x-y = 1 is given by
$d=\dfrac{\left| 2\left( -1 \right)-2-1 \right|}{\sqrt{{{2}^{2}}+{{\left( -1 \right)}^{2}}}}=\dfrac{5}{\sqrt{5}}=\sqrt{5}$
Hence we have the area of the equilateral triangle is $\dfrac{1}{2}a\times \sqrt{5}$
But the area of an equilateral triangle of side a is given by $\dfrac{\sqrt{3}}{4}{{a}^{2}}$
Hence we have
$\begin{aligned} & \dfrac{\sqrt{3}}{4}{{a}^{2}}=\dfrac{1}{2}a\sqrt{5} \\\ & \Rightarrow a=\dfrac{2\sqrt{5}}{\sqrt{3}}=\sqrt{\dfrac{20}{3}} \\\ \end{aligned}$
Hence option [a] is correct.

Note: Alternative solution:
Assume that the equation of another side of the equilateral triangle be $y-2=m\left( x+1 \right)$
Use the fact that angle between two lines of slope ${{m}_{1}}$ and ${{m}_{2}}$ is given by $\arctan \left( \dfrac{{{m}_{1}}-{{m}_{2}}}{1+{{m}_{1}}{{m}_{2}}} \right)$
Compare this angle to $\dfrac{\pi }{3}$. Hence find an equation in m.
Solve for m and hence find the slope of PB and PC.
Hence find the equation of one line of the equilateral triangle passing through (-1,2).
Solve the equation of this line and the equation of the base to get coordinates of another point of the equilateral triangle. Hence using distance formula calculate the length of the side of the triangle.