Solveeit Logo
Login

Question

Question: If the elements of given sets are given as \(n\left( A \right)=7\), \(n\left( B \right)=9\) and \(n\...

If the elements of given sets are given as n(A)=7n\left( A \right)=7, n(B)=9n\left( B \right)=9 and n(A⋃B)=14n\left( A\bigcup B \right)=14 then what is the value of n(A⋂B)n\left( A\bigcap B \right)?

Explanation

Solution

We must that the cardinal number of two individual sets, their intersection and their union Is related to each other by the equation n(A⋃B)=n(A)+n(B)−n(A⋂B)n\left( A\bigcup B \right)=n\left( A \right)+n\left( B \right)-n\left( A\bigcap B \right). Hence, by substituting all the values, we can easily find the value of n(A⋂B)n\left( A\bigcap B \right).

Complete step-by-step solution:
We know that the number of elements in any set is called the cardinal number or cardinality of that set. The cardinal number of any set A is represented as n(A), and it gives the number of elements is set A.
Here, in this question, we are given that n(A)=7n\left( A \right)=7 and n(B)=9n\left( B \right)=9. This means that the set A has 7 elements and that the set B has 9 elements.
We know that the union of two sets A and B contains all those elements that has occurred at least once either in set A or set B or both. The union of sets A and B is represented as A⋃BA\bigcup B.
We also know that the intersection of two sets A and B contains only those elements that are present in both the sets A and B. The interaction of sets A and B is represented as A⋂BA\bigcap B.

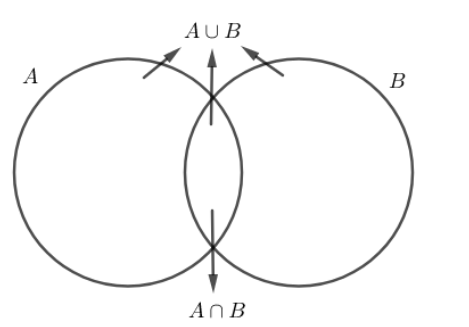
Form the above figure, we can state the following,
n(A⋃B)=n(A)+n(B)−n(A⋂B)n\left( A\bigcup B \right)=n\left( A \right)+n\left( B \right)-n\left( A\bigcap B \right)
Thus, by rearrangement, we can also write
n(A⋂B)=n(A)+n(B)−n(A⋃B)n\left( A\bigcap B \right)=n\left( A \right)+n\left( B \right)-n\left( A\bigcup B \right)
Now, by substituting the values n(A)=7n\left( A \right)=7, n(B)=9n\left( B \right)=9 and n(A⋃B)=14n\left( A\bigcup B \right)=14 in the above equation, we get
n(A⋂B)=7+9−14n\left( A\bigcap B \right)=7+9-14
Hence, we can write,
n(A⋂B)=2n\left( A\bigcap B \right)=2.
Thus, the value of n(A⋂B)n\left( A\bigcap B \right) is 2.

Note: We must be very clear with all the terminologies used in the set theory to be able to solve this problem successfully. Also, we must remember that n(A) is nothing but the number of elements in that set, which is called the cardinal number of that set.