Question
Question: If the electric field to the right of two sheets is \(\dfrac{{K\sigma }}{{{\varepsilon _0}}}\). Find...
If the electric field to the right of two sheets is ε0Kσ. Find K ?
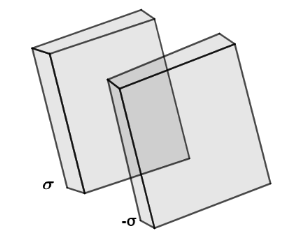
Solution
In order to solve this question we need to understand gauss law for electro statistics. According to gauss law, net flux enclosed by a closed surface is equal to net charge enclosed by surface divided by permittivity of free space ε0 also the flux is equivalent to ∮E.dS. Here, E is an electric field and dS is an elemental area vector having direction normal to the plane of the surface. Using this we can calculate electric fields across any surface.
Complete step by step answer:
Consider a plane sheet of charge having surface charge distribution σ.Then using gauss law, we get electric field around sheet as,
E=2ε0σn^
Consider a point P in right side of both sheets, then electric field at P due to plane sheet of charge distribution is, E1=2ε0σ having direction away from each other. And, electric field at P due to plane sheet of charge distribution is, E2=2ε0−σ having direction towards it.So from superposition principle, net electric field is due to,
E=E1+E2
⇒E=2ε0σ+2ε0−σ
∴E=0
So there is no electric field on the right side of both sheets.Comparing with the given value of E in question we get, K=0.
Note: It should be remembered that gauss law is only applicable for closed surfaces enclosing some net charge. Also the qnet on right hand side of gauss law implies the total charge enclosed by surface whereas the term E in left hand side of gauss law implies electric field and it is due to all charges on interior, exterior or on the closed surface.
