Question

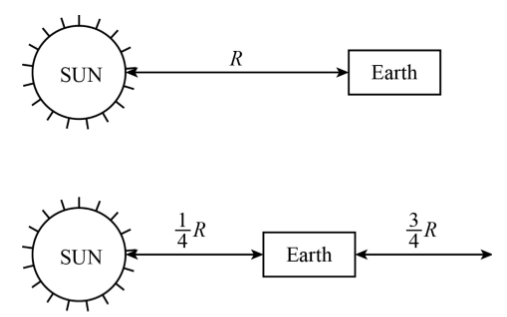
If the earth comes closer to the sun by 3/4 of the present distance, then the year of earth consists of how many days.

(A) 45.62 days
(B) 25.62 days
(C) 50.625 days
(D) 60.625 days

Answer 1

It information about the new distance is given in the question; we know that we can calculate the time period of the revolution of the earth with the help of Kepler's law. So use the Kepler's expression for the time calculation in this problem so that we can calculate the correct answer.

Complete step by step solution:
Kepler gives information about the motion of the planets in space; he gives three laws related to the planet's motion. The first tells about the planets moving around the sun in the elliptical orbit. The second law gives information about the time taken by the planets from one point to another, and the third gives is useful for us to solve this problem because it gives information about the planets orbital time that orbital time directly depends on the average distance of the planet from the sun.

From Kepler's law, write the mathematical expression for the orbital time.
${T^2} \propto {R^3}\\\ \implies T \propto \sqrt {{R^3}}$

Here, $T$ is the time and $R$ is the mean distance of the planet from the sun.
We can use the above relation for the calculation of new time if mean distance changes from its initial value.

Therefore, we get
$\dfrac{{{T_1}}}{{{T_2}}} = \dfrac{{\sqrt {R_1^3} }}{{\sqrt {R_2^3} }}$
Here, ${R_1}$ is the initial distance, ${R_2}$ is the new distance, ${T_1}$ is the original time and ${T_2}$ is the new time.
As we know that there are 365 days in one revolution, so by substituting values in the above equation, we get

$\dfrac{{365}}{{{T_2}}} = \dfrac{{\sqrt {R_1^3} }}{{\sqrt {{{\left( {\dfrac{1}{4}{R_1}} \right)}^3}} }}\\\ \implies \dfrac{{365}}{{{T_2}}} = {4^{3/2}}\\\ \implies {T_2} = \dfrac{{365}}{8}\\\ \implies {T_2} = 45.625\;{\rm{days}}$

Therefore, If the earth comes closer to the sun by 3/4 of the present distance, then the earth's year consists of 45.625 days.

So, the correct answer is “Option A”.

Note:
Remember that only Kepler's third law is useful for this problem, so use third law expression. Also, resolve the powers of the time and mean distance carefully because sometimes, we do wrong calculations during the resolution of power, and due to this, we get the wrong answer.