Question

If the domain of the function $g(x) = \log_e (\frac{2x+3}{4x^2+x-3}) + \cos^{-1}(\frac{2x-1}{x+2})$ is $(\alpha, \beta]$ and $f : [0, 3] \rightarrow A$ defined by $f(x) = 2x^3 - 15x^2 + 36x + 4\alpha + \beta + 1$ is onto, then the number of integers in the set $A$ is equal to

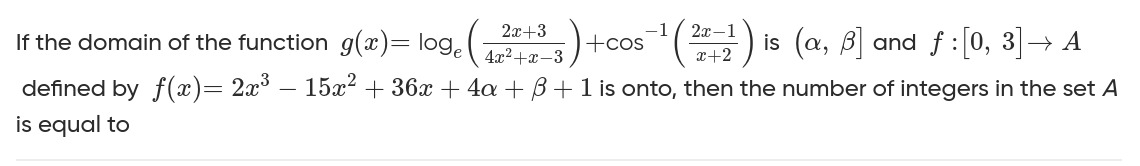
• A. 27
• B. 28
• C. 29
• D. 30

Answer 1

Answer: (C)

29

Answer 2

Here's how to solve this problem step-by-step:

1. Find the domain of g(x):

The function $g(x)$ has two parts: a logarithm and an inverse cosine. We need to consider the restrictions on each part.

• Logarithm: The argument of the logarithm must be positive: $\frac{2x+3}{4x^2+x-3} > 0$

  • Factor the denominator: $4x^2 + x - 3 = (4x - 3)(x + 1)$

  • So, we need to solve $\frac{2x+3}{(4x-3)(x+1)} > 0$. Find critical points: $x = -\frac{3}{2}, -1, \frac{3}{4}$

  • Test intervals to find where the expression is positive: $x \in (-\frac{3}{2}, -1) \cup (\frac{3}{4}, \infty)$

• Inverse Cosine: The argument of the inverse cosine must be between -1 and 1: $-1 \le \frac{2x-1}{x+2} \le 1$

  • Solve the two inequalities:

    • $\frac{2x-1}{x+2} \le 1 \Rightarrow \frac{x-3}{x+2} \le 0 \Rightarrow x \in (-2, 3]$

    • $\frac{2x-1}{x+2} \ge -1 \Rightarrow \frac{3x+1}{x+2} \ge 0 \Rightarrow x \in (-\infty, -2) \cup [-\frac{1}{3}, \infty)$

  • The domain for the inverse cosine is the intersection of these two solutions: $[-\frac{1}{3}, 3]$

• Overall Domain: The domain of $g(x)$ is the intersection of the domains of the logarithm and the inverse cosine:

  • $((-\frac{3}{2}, -1) \cup (\frac{3}{4}, \infty)) \cap [-\frac{1}{3}, 3] = (\frac{3}{4}, 3]$

  • Therefore, $\alpha = \frac{3}{4}$ and $\beta = 3$

2. Define the function f(x) and find its range:

• Substitute $\alpha$ and $\beta$ into the expression for $f(x)$:

  • $f(x) = 2x^3 - 15x^2 + 36x + 4(\frac{3}{4}) + 3 + 1 = 2x^3 - 15x^2 + 36x + 7$

• Find the critical points of $f(x)$ by taking the derivative and setting it to zero:

  • $f'(x) = 6x^2 - 30x + 36 = 6(x^2 - 5x + 6) = 6(x-2)(x-3)$

  • Critical points: $x = 2, 3$

• Evaluate $f(x)$ at the endpoints of the interval [0, 3] and at the critical points:

  • $f(0) = 7$

  • $f(2) = 2(8) - 15(4) + 36(2) + 7 = 16 - 60 + 72 + 7 = 35$

  • $f(3) = 2(27) - 15(9) + 36(3) + 7 = 54 - 135 + 108 + 7 = 34$

• The range of $f(x)$ on [0, 3] is [7, 35]. Since $f$ is onto, $A = [7, 35]$.

3. Find the number of integers in the set A:

• The integers in the set [7, 35] are 7, 8, 9, ..., 35.

• The number of integers is $35 - 7 + 1 = 29$.

Therefore, the number of integers in the set $A$ is 29.