Question

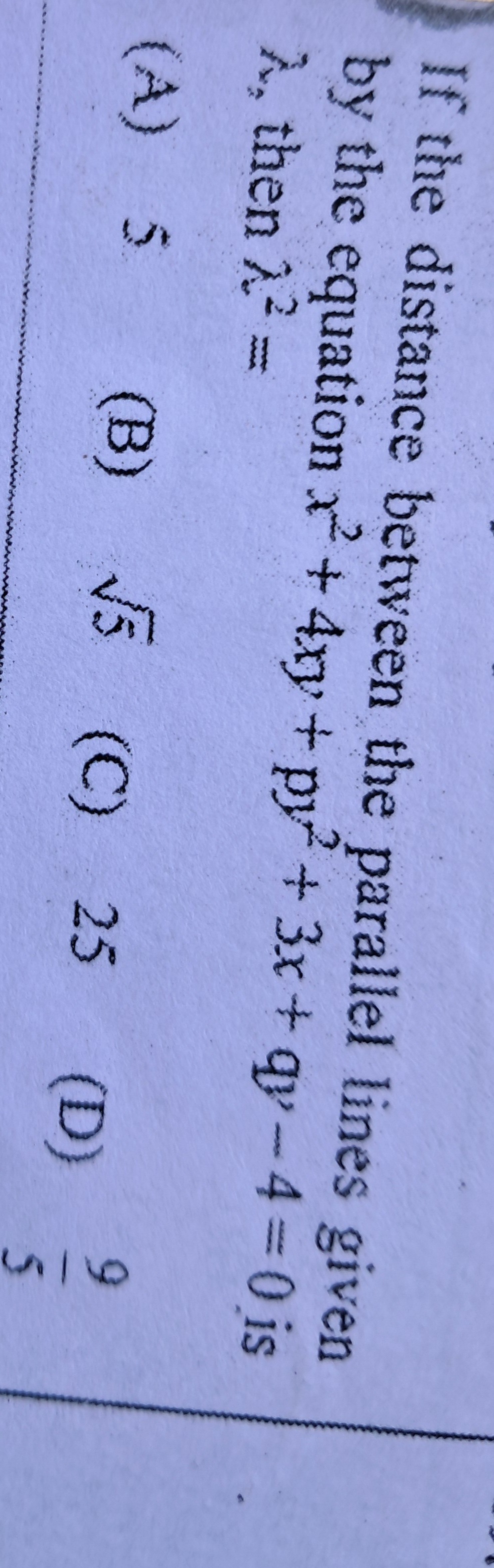
If the distance between the parallel lines given by the equation $x^2 + 4xy + y^2 + 3x + qy - 4 = 0$ is $\lambda$, then $\lambda^2 =$

• A. 5
• B. $\sqrt{5}$
• C. 25
• D. $\frac{9}{5}$

Answer 1

Answer: (A)

5

Answer 2

The given quadratic in x and y represents a pair of straight lines; its quadratic part $x^2+4xy+y^2$ is “diagonalized” by a rotation of 45° (since $tan2\theta = \infty$).

In the rotated (X,Y) coordinates the equation becomes $3X^2 – Y^2 + (3+q)/\sqrt{2} \cdot X + (q–3)/\sqrt{2} \cdot Y – 4 = 0$.

In these coordinates the two lines factor as two lines having identical directional coefficients so that they are parallel; then one shows that their separation (using the formula $|c_1–c_2|/\sqrt{(l^2+m^2)}$) has square equal to 5.