Question

If the distance between the foci of a hyperbola is 16 and its eccentricity is $\sqrt{2}$, then obtain its equation.

Answer 1

Hint: We will first let the equation of the hyperbola to be $\dfrac{{{x}^{2}}}{{{a}^{2}}}-\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$. Then we will use the fact that the distance between foci of the hyperbola is 2ae and find the value of ‘a’ from it. Then we will use the fact that eccentricity (e) of the hyperbola is $\sqrt{1+\dfrac{{{b}^{2}}}{{{a}^{2}}}}$ to find the value of b.

Complete step-by-step answer:
Now, we have been given that the distance between foci of hyperbola is 16 and its eccentricity is $\sqrt{2}$.
Now, let us take the equation of hyperbola be $\dfrac{{{x}^{2}}}{{{a}^{2}}}-\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$.

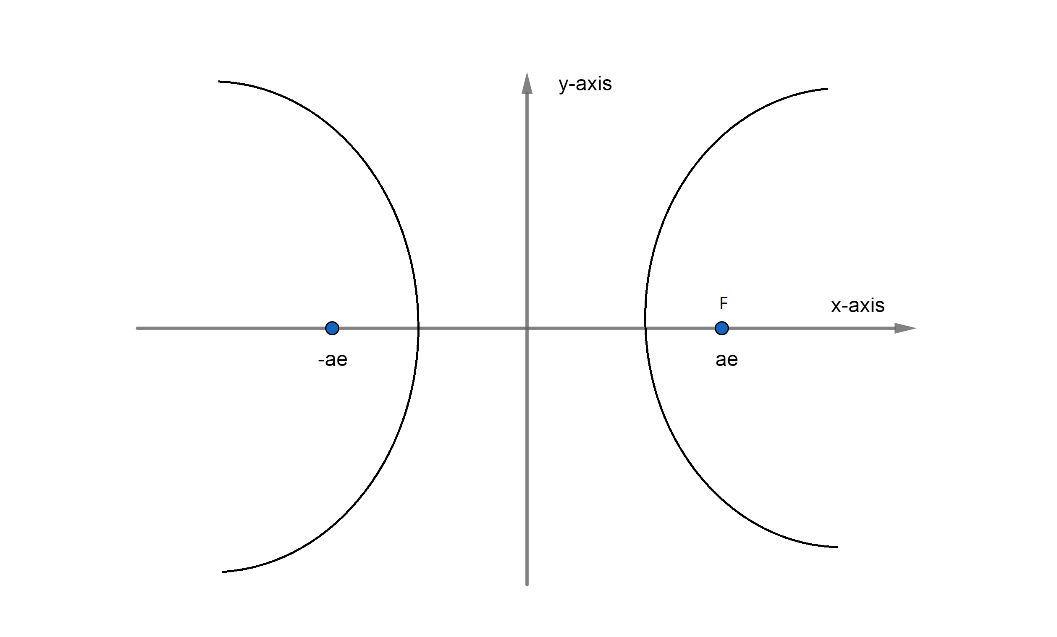
Now, we know that the distance between foci is 2ae. So, using the data given in question we have,
$\begin{aligned} & 2ae=16 \\\ & 2\times a\times e=16 \\\ \end{aligned}$
Now, we have been given $e=\sqrt{2}$. So, using this we have,
$\begin{aligned} & 2a\times \sqrt{2}=16 \\\ & a=\dfrac{8}{\sqrt{2}} \\\ & a=4\sqrt{2}...........\left( 1 \right) \\\ \end{aligned}$
Now, we know that the eccentricity of hyperbola is,
$e=\sqrt{1+\dfrac{{{b}^{2}}}{{{a}^{2}}}}$
e squaring both sides we have,
$\begin{aligned} & {{e}^{2}}=1+\dfrac{{{b}^{2}}}{{{a}^{2}}} \\\ & \left( {{e}^{2}}-1 \right){{a}^{2}}={{b}^{2}} \\\ \end{aligned}$
Now, substituting $e=\sqrt{2}$ and a from (1) we have,
$\begin{aligned} & \left( 2-1 \right)16\times 2={{b}^{2}} \\\ & 16\times 2={{b}^{2}} \\\ & {{b}^{2}}=32..........\left( 2 \right) \\\ \end{aligned}$
Now, we will substituting $a\ and\ {{b}^{2}}$ from (1) and (2) in $\dfrac{{{x}^{2}}}{{{a}^{2}}}-\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$.
So, we have the equation of hyperbola as $\dfrac{{{x}^{2}}}{32}-\dfrac{{{y}^{2}}}{32}=1$.

Note: It is important to note that the coordinates of the foci of a hyperbola $\dfrac{{{x}^{2}}}{{{a}^{2}}}-\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$ with e as eccentricity are $\left( ae,o \right),\left( -ae,o \right)$. Also, it is important to note that we have used the fact that eccentricity of hyperbola is $\sqrt{1+\dfrac{{{b}^{2}}}{{{a}^{2}}}}$.