Question

If the direction ratio of two lines are given by 3lm - 4ln + mn = 0 and l + 2m + 3n = 0, then the angle between the line is

Answer 1

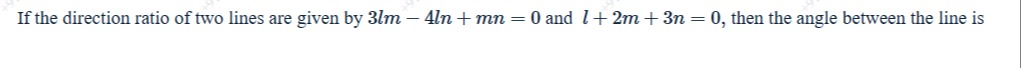
90°

Answer 2

The direction ratios $(l, m, n)$ of the two lines satisfy the given equations:

1. $3lm - 4ln + mn = 0$
2. $l + 2m + 3n = 0$

From the linear equation (2), we can express $l$ in terms of $m$ and $n$: $l = -2m - 3n$

Substitute this expression for $l$ into the first equation (1): $3(-2m - 3n)m - 4(-2m - 3n)n + mn = 0$

Expand the terms: $-6m^2 - 9mn + 8mn + 12n^2 + mn = 0$

Combine like terms: $-6m^2 + (-9mn + 8mn + mn) + 12n^2 = 0$ $-6m^2 + 0mn + 12n^2 = 0$ $-6m^2 + 12n^2 = 0$ $12n^2 = 6m^2$ $m^2 = 2n^2$

This equation gives us the relationship between $m$ and $n$. We can consider two cases based on the sign of $m$ relative to $n$. If $n=0$, then $m=0$. Substituting $m=0, n=0$ into $l+2m+3n=0$ gives $l=0$. The direction ratios $(0,0,0)$ are not valid, so $n \neq 0$. We can assume $n=1$ without loss of generality to find the direction ratios.

Case 1: $m = \sqrt{2}n$ Substitute $m = \sqrt{2}n$ into the expression for $l$: $l = -2(\sqrt{2}n) - 3n = (-2\sqrt{2} - 3)n$ The direction ratios $(l_1, m_1, n_1)$ are proportional to $(-2\sqrt{2} - 3, \sqrt{2}, 1)$ by setting $n=1$. Let $\vec{d_1} = \langle -3 - 2\sqrt{2}, \sqrt{2}, 1 \rangle$.

Case 2: $m = -\sqrt{2}n$ Substitute $m = -\sqrt{2}n$ into the expression for $l$: $l = -2(-\sqrt{2}n) - 3n = (2\sqrt{2} - 3)n$ The direction ratios $(l_2, m_2, n_2)$ are proportional to $(2\sqrt{2} - 3, -\sqrt{2}, 1)$ by setting $n=1$. Let $\vec{d_2} = \langle -3 + 2\sqrt{2}, -\sqrt{2}, 1 \rangle$.

Now we have the direction ratios of the two lines. Let $\theta$ be the angle between the lines. The cosine of the angle is given by the formula: $\cos \theta = \frac{|l_1 l_2 + m_1 m_2 + n_1 n_2|}{\sqrt{l_1^2 + m_1^2 + n_1^2} \sqrt{l_2^2 + m_2^2 + n_2^2}}$

Let's calculate the dot product $l_1 l_2 + m_1 m_2 + n_1 n_2$: $l_1 l_2 = (-3 - 2\sqrt{2})(-3 + 2\sqrt{2})$ This is in the form $(a-b)(a+b) = a^2 - b^2$, where $a = -3$ and $b = 2\sqrt{2}$. $l_1 l_2 = (-3)^2 - (2\sqrt{2})^2 = 9 - (4 \times 2) = 9 - 8 = 1$.

$m_1 m_2 = (\sqrt{2})(-\sqrt{2}) = -2$.

$n_1 n_2 = (1)(1) = 1$.

The dot product is $l_1 l_2 + m_1 m_2 + n_1 n_2 = 1 + (-2) + 1 = 0$.

Since the dot product of the direction ratios is zero, the two lines are perpendicular. The angle between perpendicular lines is $90^\circ$.

$\cos \theta = \frac{0}{\sqrt{l_1^2 + m_1^2 + n_1^2} \sqrt{l_2^2 + m_2^2 + n_2^2}} = 0$ $\theta = \cos^{-1}(0) = 90^\circ$ or $\frac{\pi}{2}$.

The final answer is $90^\circ$.