Question

If the diameter of any excircle of a triangle is equal to its perimeter then the triangle is
A) equilateral
B) isosceles
C) right angled
D) scalene

Answer 1

Hint: We will use the relation between the radius of the excircle of a triangle and its perimeter to get the desired answer.
The relation is given by:
$r1 = \dfrac{\Delta }{{\left( {s - a} \right)}}$
The diameter is twice the radius of the circle.

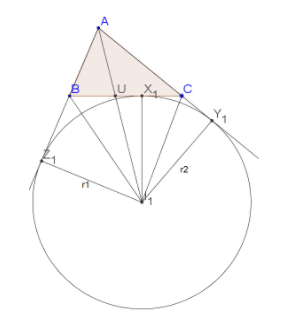
Complete step by step solution:
Here, we are given an excircle of the triangle and the diameter of the excircle is equal to the perimeter of the triangle.
Let a,b,c are the sides of the triangle then perimeter (p) of the triangle is sum of all the sides.Hence,
$p = a + b + c..............\left( 1 \right)$
Now we know that the radius of the excircle of the triangle is given by:
$r1 = \dfrac{\Delta }{{\left( {s - a} \right)}}$
Where $r1$is the radius of the excircle
$\Delta$ is the area of the triangle
Now as we know that diameter is twice the radius of the circle therefore,

$$d = 2r1 \\\ d = \dfrac{{2\Delta }}{{\left( {s - a} \right)}}................\left( 2 \right) \\\$$

Now since it is given that the diameter and the perimeter are equal therefore equating equation 1 and equation 2 we get:
$\dfrac{{2\Delta }}{{\left( {s - a} \right)}} = a + b + c$
Now as we know that:
$s = \dfrac{{a + b + c}}{2}$
Then,
$a + b + c = 2s$
Putting this value in the above equation we get:

$$\dfrac{{2\Delta }}{{\left( {s - a} \right)}} = 2s \\\ \Delta = s\left( {s - a} \right) \\\ \dfrac{\Delta }{s} = s - a \\\$$

Now, as we know that the radius of any circle is given by:
$r = \dfrac{\Delta }{s}$
Putting this value in the above equation we get:
$r = s - a............\left( 3 \right)$
Also, the radius of any circle is given by:
$r = \left( {s - a} \right)\tan \left( {\dfrac{A}{2}} \right)............\left( 4 \right)$
Where A is the angle of a triangle of which the circle is excircle.
Now equating equation 3 and equation 4 we get:

$$\left( {s - a} \right) = \left( {s - a} \right)\tan \left( {\dfrac{A}{2}} \right) \\\ \tan \left( {\dfrac{A}{2}} \right) = 1 \\\$$

Now as we know that:
$\tan \left( {\dfrac{\pi }{4}} \right) = 1$
Hence substituting the value we get:

$$\tan \left( {\dfrac{A}{2}} \right) = \tan \left( {\dfrac{\pi }{4}} \right) \\\ \left( {\dfrac{A}{2}} \right) = \left( {\dfrac{\pi }{4}} \right) \\\ A = \dfrac{\pi }{2} \\\$$

Now since we got one of the angles of the triangle to be $\dfrac{\pi }{2}$ therefore the given triangle is right angled.

Hence option (C) is the correct option.

Note:
An excircle circle of the triangle is a circle lying outside the triangle, such that one of the sides of the triangle and the extensions of the other two sides are tangent to the circle.
A triangle can have three excircles.