Question

If the diameter of a circle contains A (1,3) and B (4,5) as opposite ends. Find the equation of the line perpendicular to the diameter.

Answer 1

We will find the midpoint of the AB. then, the slope of the diameter. We will then find the slope of the line perpendicular to the line and using general form write its equation. As the center point will also satisfy the equation, we will find the value of constant.

Complete answer:
We have given the two endpoints of diameter of the circle as A(1,3) and B(4,5)
We have to find the line perpendicular to the given diameter
We will name the line as CD

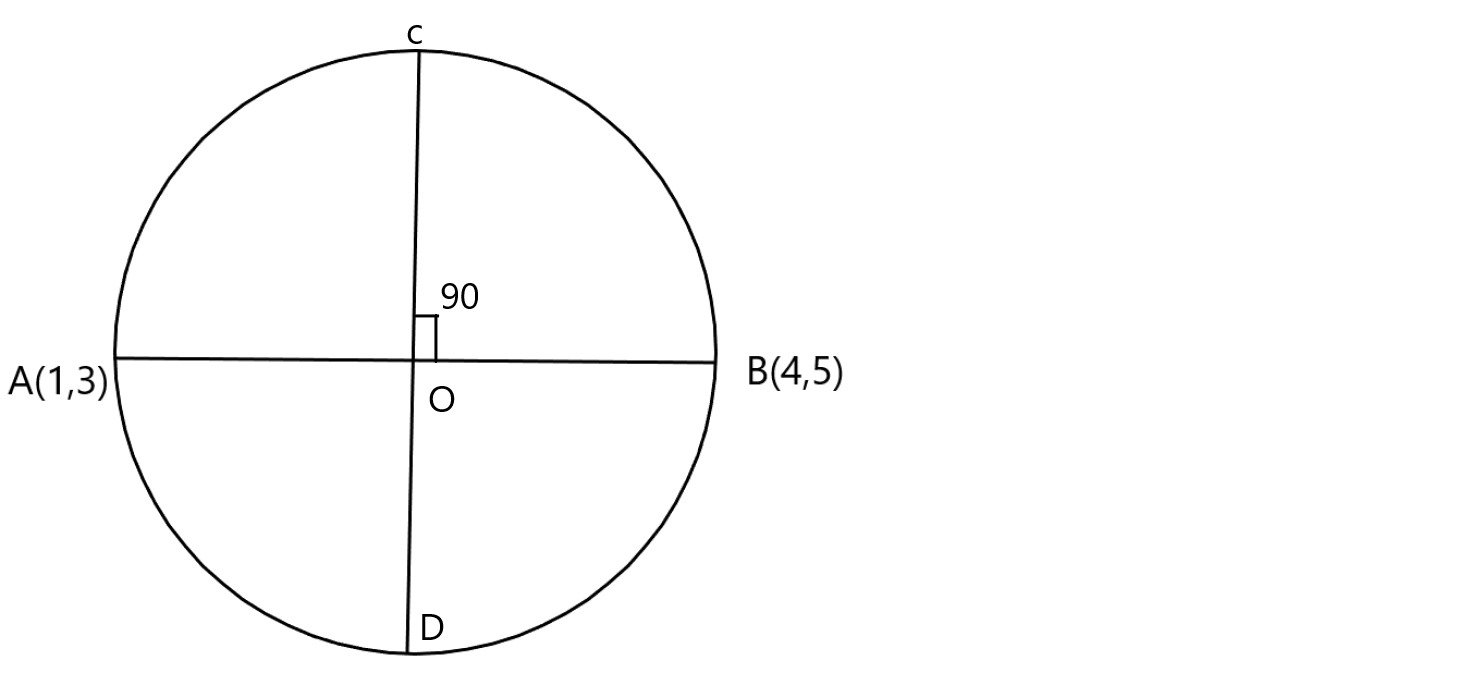
We will first find the midpoint or center of the circle.
We know that the midpoint of two point (a, b) and (c, d) is given by mid-point (M.D)
$\Rightarrow M.D = \left( {\dfrac{{a + c}}{2},\dfrac{{b + d}}{2}} \right)$
The midpoint of the point A(1,3) and B(4,5)
$\Rightarrow M.D = \left( {\dfrac{{1 + 4}}{2},\dfrac{{3 + 5}}{2}} \right)$
$\Rightarrow M.D = \left( {\dfrac{5}{2},4} \right)$
We will now find the slope of the diameter
We know that the slope of line having of two point (a, b) and (c, d) is $m = \dfrac{{d - b}}{{c - a}}$
$\Rightarrow m = \dfrac{{5 - 3}}{{4 - 1}}$
$\Rightarrow m = \dfrac{2}{3}$
We know that the slope of line perpendicular to a line having slope m is $- \dfrac{1}{m}$
So, the slope of line CD $= - \dfrac{3}{2}$
We know that the general equation is $y = mx + c$
So, the equation of line CD
$\Rightarrow y = - \dfrac{3}{2}x + c$
We will satisfy the centre with line CD as it will pass through the centre
$\Rightarrow \dfrac{5}{2} = - \dfrac{3}{2} \times 4 + c$
$\Rightarrow \dfrac{5}{2} + 6 = c$
$\Rightarrow \dfrac{{5 + 12}}{2} = c$
$\Rightarrow \dfrac{{17}}{2} = c$
So, the equation of the line CD is
$\Rightarrow y = - \dfrac{3}{2}x + \dfrac{{17}}{2}$
$\Rightarrow 2y + 3x - 17 = 0$
Hence, the equation of the line perpendicular to the line AB is $2y + 3x - 17 = 0$

Note: We should be familiar with the different formulas like how to find the midpoint of two points, to find the slope of the line. We should also be familiar with properties like the slope of a line perpendicular to a line having slope m is $- \dfrac{1}{m}$ etc.