Solveeit Logo
Login

Question

Question: If the coordinates of the vertices of the triangle ABC be (-1, 6), (-3, -9), and (5, -8) respectivel...

If the coordinates of the vertices of the triangle ABC be (-1, 6), (-3, -9), and (5, -8) respectively, then the equation of the median through C is
A. 13x−14y−47=013x-14y-47=0
B. 13x−14y+47=013x-14y+47=0
C. 13x+14y+47=013x+14y+47=0
D. 13x+14y−47=013x+14y-47=0

Explanation

Solution

Hint : This question is solved by first finding the slope of median and then applying one point form for finding the equation, that is, (y−y1)=m(x−x1)\left( y-{{y}_{1}} \right)=m\left( x-{{x}_{1}} \right) where the line passes through the point (x1,y1)\left( {{x}_{1}},{{y}_{1}} \right) and m is the slope of this line. Also, first we have to find the coordinates of midpoint by applying the formula that (x,y)=(x1+x22,y1+y22)\left( x,y \right)=\left( \dfrac{{{x}_{1}}+{{x}_{2}}}{2},\dfrac{{{y}_{1}}+{{y}_{2}}}{2} \right) where (x, y) are coordinates of mid points of (x1,y1)\left( {{x}_{1}},{{y}_{1}} \right) and (x2,y2)\left( {{x}_{2}},{{y}_{2}} \right) .

Complete step-by-step answer :
Median is the line which divides a given line into two equal parts. This means that if CD is median of line AB and D lies on the line AB then, AD = BD.

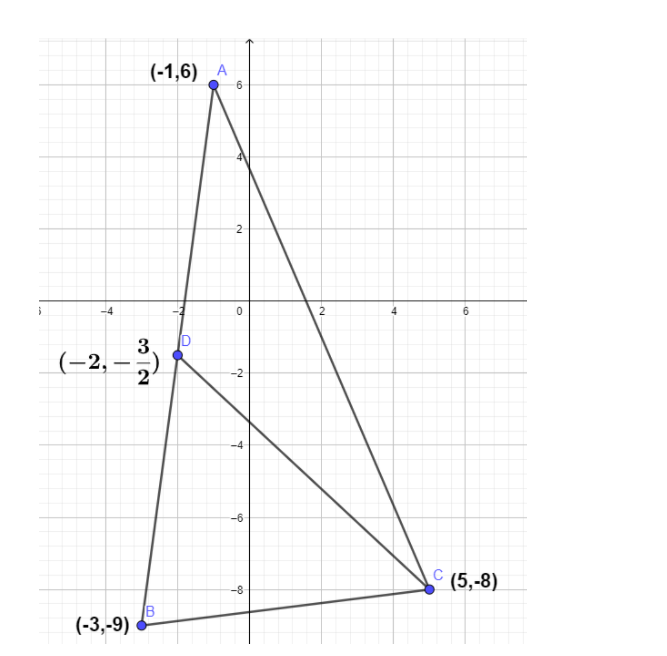
ABC is a triangle, we have to find the equation of the median through C, this means that the median through C meets AB at a point. Let that point be D, and let the coordinates of D be (x, y). We know that D is midpoint of AB so the coordinates of D is given by formula, (x,y)=(x1+x22,y1+y22)\left( x,y \right)=\left( \dfrac{{{x}_{1}}+{{x}_{2}}}{2},\dfrac{{{y}_{1}}+{{y}_{2}}}{2} \right) where x1=−1,y1=6{{x}_{1}}=-1,{{y}_{1}}=6 and x2=−3,y2=−9{{x}_{2}}=-3,{{y}_{2}}=-9 , substituting these values in above equation.
(x,y)=(−1−32,6−92)\left( x,y \right)=\left( \dfrac{-1-3}{2},\dfrac{6-9}{2} \right)
(x,y)=(−42,−32)\left( x,y \right)=\left( \dfrac{-4}{2},\dfrac{-3}{2} \right)
(x,y)=(−2,−32)(x,y)=\left( -2,\dfrac{-3}{2} \right)
This implies coordinates of D are (−2,−32)\left( -2,\dfrac{-3}{2} \right)
Now, we find slope of CD (m) which is given by formula
= (y- Coordinate of C) – (y- coordinate of D) / (x- Coordinate of C) – (x- coordinate of D)
That is,
m=−8+325+2m=\dfrac{-8+\dfrac{3}{2}}{5+2}
m=−16+327m=\dfrac{\dfrac{-16+3}{2}}{7}
m=−1314m=-\dfrac{13}{14}
Now, the equation of median CD is given by one-point form for finding the equation, that is, (y−y1)=m(x−x1)\left( y-{{y}_{1}} \right)=m\left( x-{{x}_{1}} \right) where the line passes through the point (x1,y1)\left( {{x}_{1}},{{y}_{1}} \right) and m is the slope of this line.
The median passes through the point (5, -8) and m=−1314m=-\dfrac{13}{14}
Therefore,
(y+8)=−1314(x−5)(y+8)=-\dfrac{13}{14}(x-5)
14(y+8)=−13(x−5)14(y+8)=-13(x-5)
14y+112=−13x+6514y+112=-13x+65
13x+14y+47=013x+14y+47=0
Hence, option (C) is the correct answer.
So, the correct answer is “Option C”.

Note : The main thing to keep in mind while doing such questions is to remember the formula to calculate coordinates of midpoint. And also keep in mind how to calculate the slope of a given line. One- point form should be remembered by heart. This question can also be done by using two- point form finding the equation of line if 2 points of line, which is as follow
Let (x1,y1)\left( {{x}_{1}},{{y}_{1}} \right) and (x2,y2)\left( {{x}_{2}},{{y}_{2}} \right) be two given points then the equation through them is given by (y−y1)=(x2−x1)(x−x1)(y2−y1)\left( y-{{y}_{1}} \right)=\dfrac{\left( {{x}_{2}}-{{x}_{1}} \right)\left( x-{{x}_{1}} \right)}{\left( {{y}_{2}}-{{y}_{1}} \right)}