Question

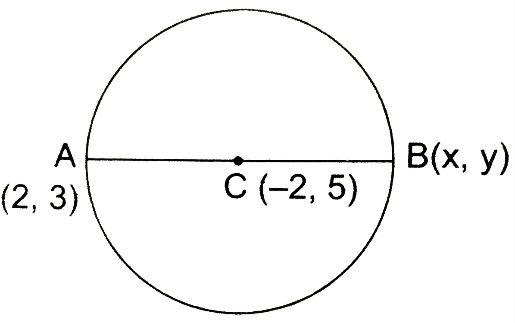
If the coordinates of the one end of the diameter of a circle are (2,3) and the coordinates of its centre are (-2,5), then the coordinates of the other end of the diameter are:
(a) (-6,7)
(b) (6,-7)
(c) (6,7)
(d) (-6,-7)

Answer 1

We will use the section formula, $\left( a,b \right)=\left( \dfrac{{{m}_{1}}{{x}_{2}}+{{m}_{2}}{{x}_{1}}}{{{m}_{1}}+{{m}_{2}}},\dfrac{{{m}_{1}}{{y}_{2}}+{{m}_{2}}{{y}_{1}}}{{{m}_{1}}+{{m}_{2}}} \right)$ where a point $\left( a,b \right)$ divides a line with end coordinates $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$ in the ratio ${{m}_{1}}:{{m}_{2}}$ , to find the other end coordinate of the diameter. We will use the fact that the centre of the circle is also the midpoint of the diameter of a circle.

Complete step by step answer:

We know if a point $\left( a,b \right)$ divides a line with end coordinates $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$ in the ratio ${{m}_{1}}:{{m}_{2}}$, then
$\left( a,b \right)=\left( \dfrac{{{m}_{1}}{{x}_{2}}+{{m}_{2}}{{x}_{1}}}{{{m}_{1}}+{{m}_{2}}},\dfrac{{{m}_{1}}{{y}_{2}}+{{m}_{2}}{{y}_{1}}}{{{m}_{1}}+{{m}_{2}}} \right)\text{ }\ldots \left( i \right)$
We also know that the centre of a circle is its midpoint. And we know diameter is a line in a circle which passes through the centre. This implies that the centre of a circle divides the diameter in two equal parts. This means that the centre of a circle divides the diameter of a circle in an equal ratio, that is, 1:1.
Thus, here,
$\begin{aligned} & \left( 2,3 \right)=\left( {{x}_{1}},{{y}_{1}} \right) \\\ & \left( -2,5 \right)=\left( a,b \right) \\\ & \left( x,y \right)=\left( {{x}_{2}},{{y}_{2}} \right) \\\ & 1:1={{m}_{1}}:{{m}_{2}} \\\ \end{aligned}$
Putting these values in equation (i), we get
$\begin{aligned} & \text{ }\left( -2,5 \right)=\left( \dfrac{1\cdot x+1\cdot 2}{1+1},\dfrac{1\cdot y+1\cdot 3}{1+1} \right) \\\ & \Rightarrow \left( -2,5 \right)=\left( \dfrac{x+2}{2},\dfrac{y+3}{2} \right) \\\ \end{aligned}$
Opening the brackets, we get
$\begin{aligned} & \text{ }\dfrac{x+2}{2}=-2 \\\ & \Rightarrow x+2=-4 \\\ & \Rightarrow x=-4-2=-6 \\\ \end{aligned}$
And,
$\begin{aligned} & \text{ }\dfrac{y+3}{2}=5 \\\ & \Rightarrow y+3=10 \\\ & \Rightarrow y=10-3=7 \\\ \end{aligned}$
Thus, the coordinates are $\left( x,y \right)=\left( -6,7 \right)$

So, the correct answer is “Option A”.

Note: We should keep a cool mind while doing calculations to make it error free. We can use the formula $\left( a,b \right)=\left( \dfrac{{{x}_{1}}+{{x}_{2}}}{2},\dfrac{{{y}_{1}}+{{y}_{2}}}{2} \right)$ directly when (a,b) is the midpoint of a line with end coordinates $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$.
For example, in this question,
$\begin{aligned} & \left( {{x}_{1}},{{y}_{1}} \right)=\left( 2,3 \right) \\\ & \left( a,b \right)=\left( -2,5 \right) \\\ & \left( {{x}_{2}},{{y}_{2}} \right)=\left( x,y \right) \\\ \end{aligned}$
Applying the formula, we get
$\left( -2,5 \right)=\left( \dfrac{x+2}{2},\dfrac{y+3}{2} \right)$
Solving this, we get
$\begin{aligned} & \text{ }\dfrac{x+2}{2}=-2 \\\ & \Rightarrow x+2=-4 \\\ & \Rightarrow x=-4-2=-6 \\\ \end{aligned}$
And, for y coordinate,
$\begin{aligned} & \text{ }\dfrac{y+3}{2}=5 \\\ & \Rightarrow y+3=10 \\\ & \Rightarrow y=10-3=7 \\\ \end{aligned}$
Thus, the coordinates are $\left( x,y \right)=\left( -6,7 \right)$
Clearly, this formula is more time-efficient.