Question

If the coordinates of the mid points of a triangle be $\left( {3, - 2} \right)$ , $\left( { - 3,1} \right)$ and $\left( {4, - 3} \right)$ , then find the coordinates of its vertices.

Answer 1

Hint : To find the vertices of the triangle, we firstly let the three vertices to be in variable form and then use the midpoint for finding the midpoints of the sides of the triangle using the considered points. After that, we just solve for both the $x$ and $y$ coordinates and obtain the vertices of the triangle.
The midpoint formula,
$P\left( {X,Y} \right) = \left( {\dfrac{{x_1 + x_2}}{2},\dfrac{{y_1 + y_2}}{2}} \right)$
Where, $x_1$ and $x_2$ are the $x$ coordinates of the end points of the line segment and $y_1$ and $y_2$ are the $y$ coordinates of the end points of the segment.

Complete step-by-step answer :
It is given that the coordinates of the mid points of the triangle are $\left( {3, - 2} \right)$ , $\left( { - 3,1} \right)$ and $\left( {4, - 3} \right)$ ,
Let the vertices be $\left( {x,y} \right)$ , $\left( {a,b} \right)$ and $\left( {d,e} \right)$

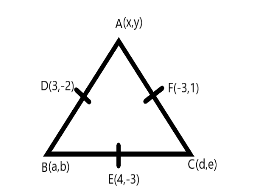
Now, in order to find the coordinates of the vertices,
We use the midpoint formula, i.e.
$P\left( {X,Y} \right) = \left( {\dfrac{{x_1 + x_2}}{2},\dfrac{{y_1 + y_2}}{2}} \right)$
So, for the side $AB$ , the midpoint, $D$ is given by
$\left( {3, - 2} \right) = \left( {\dfrac{{x + a}}{2},\dfrac{{y + b}}{2}} \right) \\\ \Rightarrow x + a = 6 \\\ y + b = - 4 - - - - \left( 1 \right) \;$
For the side $AC$ , the midpoint $F$ is given by
$\left( { - 3,1} \right) = \left( {\dfrac{{x + d}}{2},\dfrac{{y + e}}{2}} \right) \\\ \Rightarrow x + d = - 6 \\\ y + e = 2 - - - - - \left( 2 \right) \;$
For side $BC$ , the midpoint $E$ is given by
$\left( {4, - 3} \right) = \left( {\dfrac{{a + d}}{2},\dfrac{{b + e}}{2}} \right) \\\ \Rightarrow a + d = 8 \\\ b + e = - 6 - - - - - - \left( 3 \right) \;$
Solving equations $\left( 2 \right)and\left( 3 \right)$ ,
$x + d = - 6 \\\ y + e = 2 \\\ a + d = 8 \\\ b + e = - 6 \\\ \Rightarrow - 6 - x = 8 - a \\\ \Rightarrow a - x = 14 - - - - \left( 4 \right) \\\ and \; 2 - y = - 6 - b \\\ \Rightarrow b - y = - 8 - - - - - \left( 5 \right) \;$
Using $\left( 4 \right)$ and $\left( 5 \right)$ in $\left( 1 \right)$
$x + a = 6 \\\ a - x = 14 \\\ \Rightarrow 2a = 20 \\\ \Rightarrow a = 10 \\\ \therefore x = 6 - a = 6 - 10 = - 4 \;$
Solving for the values of $y$ and $b$
$y + b = - 4 \\\ b - y = - 8 \\\ \Rightarrow 2b = - 12 \\\ \Rightarrow b = - 6 \\\ \therefore y = - 4 - b = - 4 + 6 = 2 \;$
Hence the points $A$ and $B$ are $\left( { - 4,2} \right)$ and $\left( {10, - 6} \right)$ respectively.
Finding the vertex $C$ ,
From $\left( 3 \right)$ ,
$d = 8 - a = 8 - 10 = - 2$
And
$e = - 6 - b = - 6 + 6 = 0$
So, the vertex $C$ is $\left( { - 2,0} \right)$
Therefore, the coordinates of the vertices of the triangle are:
$\left( { - 4,2} \right),\left( {10, - 6} \right),\left( { - 2,0} \right)$
So, the correct answer is “ $\left( { - 4,2} \right),\left( {10, - 6} \right),\left( { - 2,0} \right)$ ”.

Note : The midpoint formula is used to find the middle point of a line segment and is obtained simply by adding the coordinates and dividing it by $2$ . This same thing is done for the $x$ coordinates and the $y$ coordinates of the end points of the segment.