Solveeit Logo
Login

Question

Question: If the complex number \(z_{1},z_{2}\)and the origin form an equilateral triangle then \(z_{1}^{2} + ...

If the complex number z1,z2z_{1},z_{2}and the origin form an equilateral triangle then z12+z22=z_{1}^{2} + z_{2}^{2} =

A

z1z2z_{1}z_{2}

B

z1zˉ2z_{1}{\bar{z}}_{2}

C

zˉ2z1{\bar{z}}_{2}z_{1}

D

∣z1∣2=∣z2∣2|z_{1}|^{2} = |z_{2}|^{2}

Answer

z1z2z_{1}z_{2}

Explanation

Solution

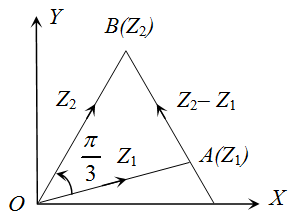
Sol. Let OA, OB be the sides of an equilateral ∆ OAB and OA, OB represent the complex numbers or vectors z1,z2z_{1},z_{2}respectively.

From the equilateral ∆ OAB, AB→=Z2−Z1\overset{\rightarrow}{AB} = Z_{2} - Z_{1}

∴ a⥂rg(z2−z1z2)=a⥂rg(z2−z1)−a⥂rgz2=π3a ⥂ rg\left( \frac{z_{2} - z_{1}}{z_{2}} \right) = a ⥂ rg(z_{2} - z_{1}) - a ⥂ rgz_{2} = \frac{\pi}{3} and

a⥂rg(z2z1)=a⥂rg(z2)−a⥂rg(z1)=π3a ⥂ rg\left( \frac{z_{2}}{z_{1}} \right) = a ⥂ rg(z_{2}) - a ⥂ rg(z_{1}) = \frac{\pi}{3}

Also, ∣z2−z1z2∣=1=∣z2z1∣,\left| \frac{z_{2} - z_{1}}{z_{2}} \right| = 1 = \left| \frac{z_{2}}{z_{1}} \right|, since triangle is equilateral.

Thus the vectors z2−z1z2\frac{z_{2} - z_{1}}{z_{2}} and z2z1\frac{z_{2}}{z_{1}}have same modulus and same argument, which implies that the vectors are equal, that is z2−z1z2=z2z1\frac{z_{2} - z_{1}}{z_{2}} = \frac{z_{2}}{z_{1}} ⇒ z1z2−z12=z22z_{1}z_{2} - z_{1}^{2} = z_{2}^{2} ⇒ z12+z22=z1z2.z_{1}^{2} + z_{2}^{2} = z_{1}z_{2}.