Question

If the common tangents to the parabola, ${x^2} = 4y$ and the circle, ${x^2} + {y^2} = 4$ intersect at the point P, then find the square of the slope of the line:
A $3 + 2\sqrt 2$
B $2\left( {3 + 2\sqrt 2 } \right)$
C $2(\sqrt 2 + 1)$
D $\sqrt 2 + 1$

Answer 1

In this question we have been given a parabola ${x^2} = 4y$and the circle ${x^2} + {y^2} = 4$, and if they intersect at a point P, then we need to find the square of the slope of the line, for that we will be finding the tangent the circle using the formula: $y = mx + c$, after that we will but that value of y in the equation of parabola, from which we can easily find the square of the root.

Complete step by step answer:

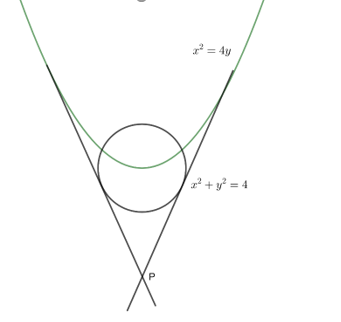
We have been provided with a parabola ${x^2} = 4y$ and the circle ${x^2} + {y^2} = 4$,
So, firstly we will be finding the equation of tangent to the circle using the formula: $y = mx + c$,
Also, we know the condition for tangency for slope-form: $y = mx \pm r\sqrt {1 + {m^2}}$, where m = slope
r = radius.
According to the question, radius =2 from ${x^2} + {y^2} = 4$,
So, now we will be putting the values in $y = mx \pm r\sqrt {1 + {m^2}}$,
So, the value comes out to be: $y = mx \pm 2\sqrt {1 + {m^2}}$,
Also, we have been given a parabola ${x^2} = 4y$,
So, keeping this value of y in $y = mx \pm r\sqrt {1 + {m^2}}$,
Now the equation would become: ${x^2} = 4mx \pm 8\sqrt {1 + {m^2}}$,
Now if we put (D) = 0, the equation would become: $16{m^2} - 32\sqrt {1 + {m^2}} = 0$ using the formula: $D = {b^2} - 4ac$,
Now taking 16 common we get: ${m^2} - 2\sqrt {1 + {m^2}} = 0$
Now, squaring both sides: ${m^4} - 4(1 + {m^2}) = 0$
Now the equation becomes: ${m^4} - 4{m^2} - 4 = 0$,
Now we will be factorizing the above equation using the formula: $\dfrac{{ - b \pm \sqrt {{b^2} - 4ac} }}{2}$, where a=1, b=-4 and c=-4,
Putting the values, we will get: ${m^2} = \dfrac{{4 \pm \sqrt {16 + 16} }}{2}$,
From this we will get the value: ${m^2} = \dfrac{{4 \pm 4\sqrt 2 }}{2}$,
But here the square of the slope needs to be positive so: ${m^2} = \dfrac{{4 + 4\sqrt 2 }}{2}$,
Now solving the equation further, we get: ${m^2} = 2 + \sqrt 2$,
Therefore, the square of the slope comes out to be: ${m^2} = 2(\sqrt 2 + 1)$,
From this we can say that option (c) is correct.

Note:
In this question, be cautious while finding the square of the slope and exclude the negative values. Also, don’t just use the straight-line equation $y = mx + c$ to find the slope, as we need to find the equation of tangent as well by using the formula: $y = mx \pm r\sqrt {1 + {m^2}}$