Question

If the coefficient of friction is $\sqrt 3$ , the angle of friction is
A) $30^\circ$
B) $60^\circ$
C) $45^\circ$
D) $37^\circ$

Answer 1

The coefficient of friction between two surfaces is the tangent of the angle at which the object overcomes friction force and starts sliding. It can also be defined as the tangent of the angle of friction.
Formula used: $\tan \theta = \mu$ where $\tan \theta$ is the angle of friction and $\mu$ is the coefficient of friction.

Complete step by step solution:
When a body experiences a friction force ${F_f}$, the angle of friction $\theta$ can be seen in the diagram below:

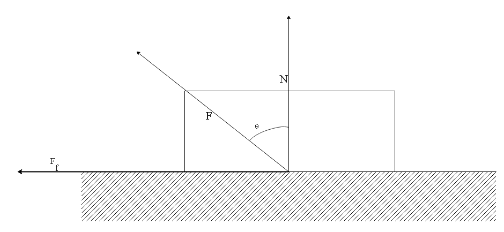
The coefficient of friction $\mu$ is defined as the ratio of the friction force ${F_f}$ to the normal force $N$. Hence, we can write:
$\Rightarrow \mu = \dfrac{{{F_f}}}{N}$ ......(1)
Now, from the schematic diagram of the block, we can calculate the value of $\tan \theta$ as the ratio of force in the horizontal direction to the ratio of the force in the vertical direction. Since the friction force ${F_f}$acts in the horizontal direction and the Normal force $N$ acts in the vertical direction, we can write
$\Rightarrow \tan \theta = \dfrac{{{F_f}}}{N}$ ......(2)
Equating equations (1) and (2), we can write
$\Rightarrow \tan \theta = \mu$
Hence, if the coefficient of friction $\mu = \sqrt 3$ , then
$\Rightarrow \tan \theta = \sqrt 3$
Taking the inverse tangent on both sides, we get:
$\Rightarrow \theta = {\tan ^{ - 1}}(\sqrt 3 )$
$\therefore \theta = 60^\circ$
Hence the angle of friction corresponding to the coefficient of friction $\sqrt 3$ is equal to $60^\circ$ which corresponds to option (B).

Hence, the correct option is option (B).

Additional Information:
Since the coefficient friction of any surface can only lie between 0 and 1, the angle of friction can lie only between $0^\circ$ and $90^\circ$.

Note:
The relation between coefficient of friction and angle of friction should be known to solve this problem. The angle of friction corresponds to the maximum static friction force between two surfaces and if the angle $\theta$ between the block and the surface is less than the angle of friction, the block will start sliding on the surface.