Question
Question: If the coefficient of friction between an insect and bowl surface is $\mu$ and the diameter of bowl ...
If the coefficient of friction between an insect and bowl surface is μ and the diameter of bowl is r. Find the maximum height to which the insect can crawl in the bowl :-
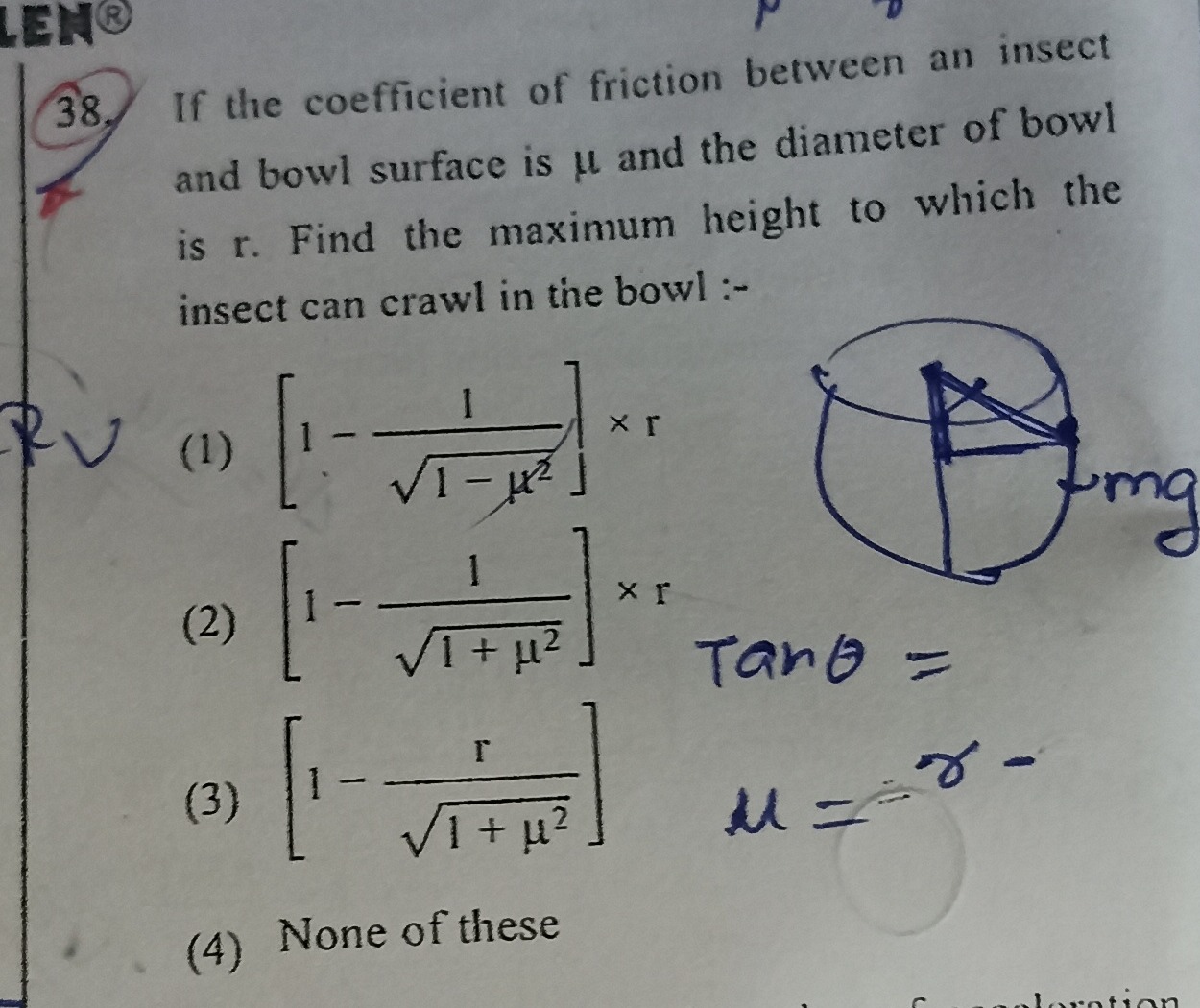
[1−1−μ21]×r
[1−1+μ21]×r
[1−1+μ2r]
None of these
(2)
Solution
To find the maximum height to which the insect can crawl, we consider the forces acting on the insect when it is on the verge of slipping.
Let the radius of the hemispherical bowl be R. Let the insect be at a point P on the surface, such that the line connecting the center O to the insect P makes an angle θ with the vertical. The height of the insect from the bottom of the bowl is h.
Forces acting on the insect:
- Weight (mg): Acts vertically downwards.
- Normal Force (N): Acts perpendicular to the surface, outwards from the center O.
- Frictional Force (f): Acts tangentially upwards along the surface, opposing the tendency of the insect to slide downwards due to gravity.
Resolution of Forces: We resolve the weight mg into two components:
- Component along the radius (normal to the surface), pointing towards the center: mgcosθ.
- Component tangential to the surface, pointing downwards along the tangent: mgsinθ.
For equilibrium in the normal direction (perpendicular to the surface): The normal force N balances the radial component of the weight. N=mgcosθ(Equation 1)
For the insect to be able to crawl up to the maximum height, it must be on the verge of slipping. At this point, the tangential component of the weight is balanced by the maximum static friction. The maximum static frictional force is given by fmax=μN, where μ is the coefficient of friction. So, for the insect to be at the maximum height without slipping: mgsinθ=fmax mgsinθ=μN(Equation 2)
Determining the maximum angle θ: Substitute Equation 1 into Equation 2: mgsinθ=μ(mgcosθ) Divide both sides by mgcosθ (assuming cosθ=0): cosθsinθ=μ tanθ=μ This gives the maximum angle θ at which the insect can stay without slipping.
Calculating the maximum height h: From the geometry of the bowl, the vertical distance from the center O to the insect's position is Rcosθ. The total height of the bowl from its bottom is equal to its radius R. Therefore, the height h to which the insect can crawl from the bottom of the bowl is: h=R−Rcosθ h=R(1−cosθ)
Now, we need to express cosθ in terms of μ. We know tanθ=μ. Using the trigonometric identity sec2θ=1+tan2θ: sec2θ=1+μ2 Since secθ=cosθ1, we have: cos2θ1=1+μ2 cos2θ=1+μ21 Since θ is an acute angle (as the insect crawls up from the bottom), cosθ is positive: cosθ=1+μ21
Substitute this expression for cosθ into the equation for h: h=R(1−1+μ21)
Interpreting the given radius/diameter: The problem states "the diameter of bowl is r". This means the radius of the bowl is R=r/2. If we substitute R=r/2 into our derived formula for h: h=2r(1−1+μ21) However, none of the given options exactly match this form.
Let's re-examine the options and a common convention in such physics problems. Often, 'r' is used to denote the radius of a spherical or circular object in the options, even if the question text ambiguously refers to it as diameter. If we assume that 'r' in the options (and implicitly in the question, for consistency with options) refers to the radius of the bowl (i.e., R=r), then: h=r(1−1+μ21) This exactly matches option (2). Given that options (1) and (3) are mathematically or dimensionally incorrect, option (2) is the most plausible answer.
The final answer is (2)
Explanation of the solution:
- Identify forces: Weight (mg), Normal force (N), and Frictional force (f).
- Resolve weight into components normal (mgcosθ) and tangential (mgsinθ) to the bowl surface, where θ is the angle with the vertical.
- For equilibrium, N=mgcosθ.
- At maximum height, the tangential component of weight is balanced by maximum static friction: mgsinθ=μN.
- Substitute N to get mgsinθ=μ(mgcosθ), which simplifies to tanθ=μ.
- The height h from the bottom of the bowl of radius R is h=R−Rcosθ=R(1−cosθ).
- Express cosθ in terms of μ using tanθ=μ and sec2θ=1+tan2θ: cosθ=1+μ21.
- Substitute cosθ into the height formula: h=R(1−1+μ21).
- Assuming 'r' in the question refers to the radius of the bowl (as is common in physics problems and consistent with option 2), R=r.
- Thus, the maximum height is h=r(1−1+μ21).
