Question

If the coefficient of friction between A and B is $\mu$. The maximum horizontal acceleration of the wedge A for which B will remain at rest w.r.t the wedge is

A. $\mu g$
B. $g(\dfrac{{1 + \mu }}{{1 - \mu }})$
C. $\dfrac{g}{\mu }$
D. $g(\dfrac{{1 - \mu }}{{1 + \mu }})$

Answer 1

Try to solve by taking A as a frame of reference and use pseudo force concept it will be easy that way you can also solve by taking ground as a frame of reference but then you will have to apply constraint equations which will make it little complex.

Complete step by step answer:
We will solve this question by taking wedge A as a frame of reference.
So free body diagram according as we observe B from A will be

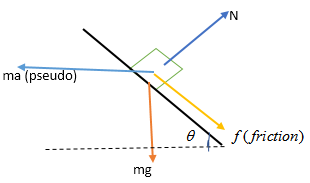
balancing force perpendicular to incline we have,
$N = mg\cos \theta + ma\sin \theta$so
Friction $f = \mu N = \mu (mg\cos \theta + ma\sin \theta )$
And balancing force along the incline we have,
$f + mg\sin \theta = ma\cos \theta$
$\Rightarrow \mu (mg\cos \theta + ma\sin \theta ) + mg\sin \theta = ma\cos \theta$
$\Rightarrow a = \dfrac{{g\sin \theta + \mu g\cos \theta }}{{a\cos \theta - \mu a\sin \theta }}$ putting $\theta = {45^ \circ }$we have
$\therefore a = g(\dfrac{{1 + \mu }}{{1 - \mu }})$

So, the correct answer is “Option B”.

Note:
In these types of questions, choosing a frame of reference is critical because choosing a better frame of reference makes a lot of things easy here. For example, once we take wedge A as a frame of reference we won’t have to worry about constraint equations and it makes it easier to solve such questions.