Question

If the coefficient of friction between $A$ and $B$ is $$ , the maximum acceleration of the wedge $A$ for which $B$ will remain at rest with respect to the wedge is

(A) $g$
(B) $g(\dfrac{{1 + \mu }}{{1 - \mu }})$
(C) $\dfrac{g}{\mu }$
(D) $g(\dfrac{{1 - \mu }}{{1 + \mu }})$

Answer 1

Hint
For the body to remain at rest the friction force should be equal or lesser than the force acting on the body due to the acceleration of the wedge. At the point just before the body starts to move is the maximum acceleration of the wedge for which the body remains at rest.
To solve the problem, we have four forces acting on the body, the weight of the body, the normal force, the friction force, and the force due to acceleration of the wedge. We resolve these forces into its horizontal and vertical components then add them up and equate it to zero to get the maximum acceleration.
Friction force $f = \mu {F_N}$
Here, Coefficient of friction is represented by $\mu$
Friction force is represented by $f$
Normal force is represented by ${F_N}$

Complete step by step answer
The free-body diagram of the system is

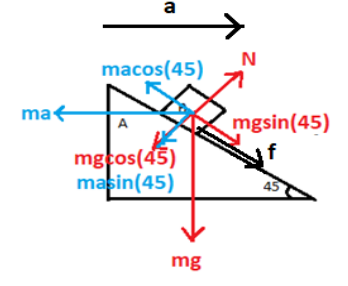
From the diagram we can see that the weight of the body $mg$ is resolved into its horizontal and vertical components. $mg\cos(\theta ),mg\sin (\theta )$
The angle with which it is resolved is the angle of the wedge. That is $45^\circ$
The wedge along with the box is being accelerated forward but due to the inclination of the wedge the resultant force $ma$ acting on the box is in the opposite direction of the acceleration $a$ resolving this force into its components we get $ma\sin (\theta ),ma\cos (\theta )$ . The angle between the force acting on the box and its horizontal component is equal to the angle of inclination of the wedge.
Based on the direction of the forces acting on the body
The normal force is the sum of
${F_N} = ma\sin (45^\circ ) + mg\cos (45^\circ )$
Friction force
$\Rightarrow f = \mu {F_N}$
$\Rightarrow f = \mu [ma\sin (45^\circ ) + mg\cos (45^\circ )]$
We know that for the body to be at rest the sum of all the forces on the body should be equal to zero
$\Rightarrow \mu (ma\sin (45^\circ ) + mg\cos (45^\circ )) + mg\sin (45^\circ ) – ma\cos(45^\circ ) = 0$
$\Rightarrow \mu (a\sin (45^\circ ) + g\cos (45^\circ )) + g\sin (45^\circ ) – a\cos(45^\circ ) = 0$
$\Rightarrow g(\mu + 1) - a(1 - \mu ) = 0$
$\Rightarrow a = \dfrac{{g(\mu + 1)}}{{1 - \mu }}$
The maximum acceleration of the wedge for which the box remains at rest is $a = \dfrac{{g(\mu + 1)}}{{1 - \mu }}$
Hence option (B) $a = \dfrac{{g(\mu + 1)}}{{1 - \mu }}$ is the correct answer.

Note
Students might make a mistake by taking the direction of force acting on the box the same as the direction of acceleration of the wedge. Due to the inclination of the wedge, the force acting on the box is in the opposite direction of the acceleration of the wedge. The friction force that is causing the body to remain at rest is called static friction force. The formula to find it is the same as that of friction force.