Solveeit Logo
Login

Question

Question: If the circumradius and inradius of a triangle be 10 and 3 respectively, then the value of a cot A +...

If the circumradius and inradius of a triangle be 10 and 3 respectively, then the value of a cot A + b cot B + c cot C is equal to 25.
(a) True
(b) False

Explanation

Solution

Hint:First of all, draw the diagram to visualize the question. Now, write a = 2R sin A, b = 2R sin B, c = 2R sin C and also, cot⁡θ=cos⁡θsin⁡θ\cot \theta =\dfrac{\cos \theta }{\sin \theta } in the given expression. Now, proceed with solving the expression and finally substitute 4sin⁡A2sin⁡B2sin⁡C2=rR4\sin \dfrac{A}{2}\sin \dfrac{B}{2}\sin \dfrac{C}{2}=\dfrac{r}{R} to get the desired value.

Complete step-by-step answer:
We are given that the circumradius and inradius of a triangle be 10 and 3 respectively, then we have to verify if a cot A + b cot B + c cot C is equal to 25 or not. Let us see what inradius and circumradius are by the diagram.

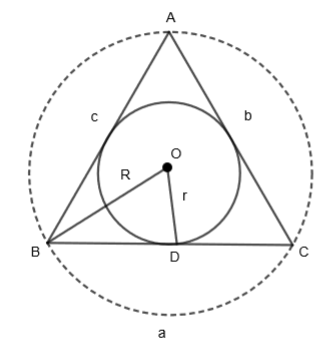
In the above figure, OB is the circumradius (R) of ΔABC\Delta ABC and OD is the inradius (r) of ΔABC\Delta ABC. Also, a, b and c are the sides of ΔABC\Delta ABC. Here, we are given that R = OB = 10. Also, R = OB = OC = OA = 10 as all the radii are of the same length.
We are also given that r = OD = 3. Now, let us consider the expression given in the question.
E = a cot A + b cot B + c cot C
We know that cot⁡θ=cos⁡θsin⁡θ\cot \theta =\dfrac{\cos \theta }{\sin \theta }. So by using this in the above equation, we get,
E=acos⁡Asin⁡A+bcos⁡Bsin⁡B+ccos⁡Csin⁡CE=a\dfrac{\cos A}{\sin A}+b\dfrac{\cos B}{\sin B}+c\dfrac{\cos C}{\sin C}
Now, we know that, a = 2R sin A, b = 2R sin B, c = 2R sin C. By substituting them in the above equation, we get,
E=2Rsin⁡Acos⁡Asin⁡A+2Rsin⁡Bcos⁡Bsin⁡B+2Rsin⁡Ccos⁡Csin⁡CE=2R\sin A\dfrac{\cos A}{\sin A}+2R\sin B\dfrac{\cos B}{\sin B}+2R\sin C\dfrac{\cos C}{\sin C}
By cancelling the like terms from the above equation, we get,
E=2Rcos⁡A+2Rcos⁡B+2Rcos⁡CE=2R\cos A+2R\cos B+2R\cos C
E=2R(cos⁡A+cos⁡B+cos⁡C)E=2R\left( \cos A+\cos B+\cos C \right)
Now, we know that,
cos⁡x+cos⁡y=2cos⁡(x+y2)cos⁡(x−y2)\cos x+\cos y=2\cos \left( \dfrac{x+y}{2} \right)\cos \left( \dfrac{x-y}{2} \right)
Also, cos⁡x=1−2sin⁡2x2\cos x=1-2{{\sin }^{2}}\dfrac{x}{2}. By using this in the above equation, we get,
E=2R[2cos⁡(A+B2)cos⁡(A−B2)+1−2sin⁡2C2]E=2R\left[ 2\cos \left( \dfrac{A+B}{2} \right)\cos \left( \dfrac{A-B}{2} \right)+1-2{{\sin }^{2}}\dfrac{C}{2} \right]
We know that for any triangle,
A+B+C=πA+B+C=\pi
A+B=π−CA+B=\pi -C
By using this, we get,
E=2R[2cos⁡(π−C2)cos⁡(A−B2)+1−2sin⁡2C2]E=2R\left[ 2\cos \left( \dfrac{\pi -C}{2} \right)\cos \left( \dfrac{A-B}{2} \right)+1-2{{\sin }^{2}}\dfrac{C}{2} \right]
We know that,
cos⁡(π2−θ)=sin⁡θ\cos \left( \dfrac{\pi }{2}-\theta \right)=\sin \theta
So, by using this, we get,
E=2R[2sin⁡C2cos⁡(A−B2)+1−2sin⁡2C2]E=2R\left[ 2\sin \dfrac{C}{2}\cos \left( \dfrac{A-B}{2} \right)+1-2{{\sin }^{2}}\dfrac{C}{2} \right]
We can write the above equation as,
E=2R[1+2sin⁡C2(cos⁡(A−B2)−sin⁡C2)]E=2R\left[ 1+2\sin \dfrac{C}{2}\left( \cos \left( \dfrac{A-B}{2} \right)-\sin \dfrac{C}{2} \right) \right]
By replacing C by π−(A+B)\pi -\left( A+B \right) in the second bracket, we get,
E=2R[1+2sin⁡C2(cos⁡(A−B2)−sin⁡(π2−(A+B2)))]E=2R\left[ 1+2\sin \dfrac{C}{2}\left( \cos \left( \dfrac{A-B}{2} \right)-\sin \left( \dfrac{\pi }{2}-\left( \dfrac{A+B}{2} \right) \right) \right) \right]
We know that sin⁡(π2−θ)=cos⁡θ\sin \left( \dfrac{\pi }{2}-\theta \right)=\cos \theta . By using this, we get,
E=2R[1+2sin⁡C2(cos⁡(A−B2)−cos⁡(A+B2))]E=2R\left[ 1+2\sin \dfrac{C}{2}\left( \cos \left( \dfrac{A-B}{2} \right)-\cos \left( \dfrac{A+B}{2} \right) \right) \right]
We know that,
cos⁡x−cos⁡y=−2sin⁡(x+y2)sin⁡(x−y2)\cos x-\cos y=-2\sin \left( \dfrac{x+y}{2} \right)\sin \left( \dfrac{x-y}{2} \right)
By using this, we get,
E=2R[1+2sin⁡C2[−2sin⁡((A−B2)+(A+B2)2)sin⁡((A−B2)−(A+B2)2)]]E=2R\left[ 1+2\sin \dfrac{C}{2}\left[ -2\sin \left( \dfrac{\left( \dfrac{A-B}{2} \right)+\left( \dfrac{A+B}{2} \right)}{2} \right)\sin \left( \dfrac{\left( \dfrac{A-B}{2} \right)-\left( \dfrac{A+B}{2} \right)}{2} \right) \right] \right]
E=2R[1+2sin⁡C2(−2sin⁡(A2)sin⁡(−B2))]E=2R\left[ 1+2\sin \dfrac{C}{2}\left( -2\sin \left( \dfrac{A}{2} \right)\sin \left( \dfrac{-B}{2} \right) \right) \right]
We know that sin⁡(−θ)=−sin⁡θ\sin \left( -\theta \right)=-\sin \theta . By using this, we get,
E=2R[1+4sin⁡C2.sin⁡A2.sin⁡B2]E=2R\left[ 1+4\sin \dfrac{C}{2}.\sin \dfrac{A}{2}.\sin \dfrac{B}{2} \right]
Now, we know that for any triangle ABC, inradiuscircumradius\dfrac{\text{inradius}}{\text{circumradius}}=4sin⁡A2sin⁡B2sin⁡C24\sin \dfrac{A}{2}\sin \dfrac{B}{2}\sin \dfrac{C}{2}
Or, rR=4sin⁡A2sin⁡B2sin⁡C2\dfrac{r}{R}=4\sin \dfrac{A}{2}\sin \dfrac{B}{2}\sin \dfrac{C}{2}
By using this we get,
E=2R(1+rR)E=2R\left( 1+\dfrac{r}{R} \right)
E=2R+2rE=2R+2r
By substituting the values of R = 10 and r = 3. We get,
E=2(10)+2(3)E=2\left( 10 \right)+2\left( 3 \right)
E=20+6E=20+6
E=26E=26
Hence, the value of a cot A + b cos B + c cot C = 26.
So, given the value of the expression is false.

Note: In these types of questions, students can directly remember that for a triangle ABC, (cos A + cos B + cos C) is equal to 1+rR1+\dfrac{r}{R}. This is a very useful result in the solution of the triangle and would save a lot of steps. In this question, students often make mistakes while adding angles. So, this must be avoided.