Question

If the circle ${x^2} + {y^2} = {a^2}$ cut off an intercept of length $2l$ units from the line $y = mx + c$ then
$A.{c^2} = \left( {{a^2} + {l^2}} \right)\left( {1 + {m^2}} \right) \\\ B.{c^2} = \left( {1 + {m^2}} \right)\left( {{a^2} - {l^2}} \right) \\\ C.{a^2} = \left( {{c^2} + {l^2}} \right)\left( {1 + {m^2}} \right) \\\ D.{a^2} = \left( {{c^2} - {l^2}} \right)\left( {1 + {m^2}} \right) \\\$

Answer 1

Equation of a circle is a way to express the definition of a circle on the coordinate plane given by ${\left( {x - h} \right)^2} + {\left( {y - k} \right)^2} = {r^2}$, where (h, k) represents the center of the circle and r being the length of the radius from the center of the circle (h, k).
When a straight line passes anywhere through a circle then the part of the line inside the circle is called chord. It only covers a part of the circle and if the chord passes through the center of the circle then it is known as the diameter.
In the question the straight line $y = mx + c$ passes through the circle ${x^2} + {y^2} = {a^2}$ the part if the line passing from inside circle is chord whose equation will be equal to$2l$.

Complete step by step solution:
Given the equation of the circle ${x^2} + {y^2} = {a^2}$ whose center is at the origin $\left( {0,0} \right)$ and radius $r = a$
Straight line $y = mx + c$ is passing through the circle and the section of the line inside the circle is chord which is equal to $2l$

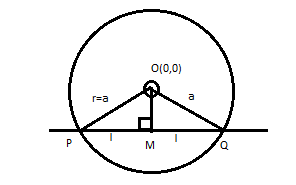
When a line is drawn from the center of circle perpendicular to the chord then the line divides chord into two parts$MQ = l$,
Now considering the $\vartriangle OMP$ which is a right angle triangle use the Pythagoras theorem to find the length of OM, let OM=l

$$O{M^2} + P{M^2} = O{P^2} \\\ {d^2} = {a^2} - {l^2} - - - - (i) \\\$$

Now find the distance d of line OM by using distance formula between O (0,0) and the straight line $y = mx + c$, we can write $mx - y + c = 0$

$$d = \left| {\dfrac{{m \times 0 - 0 + c}}{{\sqrt {{m^2} + {{\left( { - 1} \right)}^2}} }}} \right| \\\ = \left| {\dfrac{c}{{\sqrt {1 + {m^2}} }}} \right| \\\$$

Now put d in equ (i) we get

$${d^2} = {a^2} - {l^2} \\\ {\left( {\left| {\dfrac{c}{{\sqrt {1 + {m^2}} }}} \right|} \right)^2} = {a^2} - {l^2} \\\ \dfrac{{{c^2}}}{{1 + {m^2}}} = {a^2} - {l^2} \\\$$

Hence we can write

$$\dfrac{{{c^2}}}{{1 + {m^2}}} = {a^2} - {l^2} \\\ {c^2} = \left( {{a^2} - {l^2}} \right)\left( {1 + {m^2}} \right) \\\$$

Option (B) is correct.

Note:
When a straight line passes anywhere through a circle then the part of the line inside the circle is called chord. A chord is a straight line segment whose endpoints lie on the circle. “Every diameter is a chord but every chord is not a diameter”. Diameters are the chords that should pass through the center of the circle only whereas there is no such limit for the chord.