Question

If the chord of contact of tangents from a point on the circle ${{x}^{2}}+{{y}^{2}}={{a}^{2}}$ to the circle ${{x}^{2}}+{{y}^{2}}={{b}^{2}}$ touches the circle ${{x}^{2}}+{{y}^{2}}={{c}^{2}}$, then a, b, c are in
(a) AP
(b) GP
(c) HP
(d) None of these

Answer 1

Hint: First, draw a diagram. Let P (x1​, y1​) be any point on the circle ${{x}^{2}}+{{y}^{2}}={{a}^{2}}$. The equation of the chord of contact of tangents from P (x1​, y1​) to the circle is $x{{x}_{1}}+y{{y}_{1}}={{b}^{2}}$. Find the length of perpendicular from centre (0, 0) to the chord of contact $x{{x}_{1}}+y{{y}_{1}}={{b}^{2}}$ using the formula $\dfrac{|lp+mq+n|}{\sqrt{{{l}^{2}}+{{m}^{2}}}}$ and equate it to c. simplify this to get the final answer.

Complete step-by-step answer:
In this question, we are given that the chord of contact of tangents from a point on the circle ${{x}^{2}}+{{y}^{2}}={{a}^{2}}$ to the circle ${{x}^{2}}+{{y}^{2}}={{b}^{2}}$ touches the circle ${{x}^{2}}+{{y}^{2}}={{c}^{2}}$.
Using this information, we need to find the relationship between a, b, and c.
As we can see from the equations of the circles, all the three circles have the same centre at the origin: (0, 0) i.e. they are concentric.
First, we will draw a diagram to understand and visualise the question better.

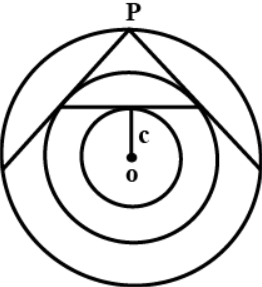
Here, the outermost circle is ${{x}^{2}}+{{y}^{2}}={{a}^{2}}$, the innermost circle is ${{x}^{2}}+{{y}^{2}}={{c}^{2}}$, and the middle circle is ${{x}^{2}}+{{y}^{2}}={{b}^{2}}$.
Let P (x1​, y1​) be any point on the circle ${{x}^{2}}+{{y}^{2}}={{a}^{2}}$.
Then, ${{x}_{1}}^{2}+{{y}_{1}}^{2}={{a}^{2}}$ …(1)
We know that the equation of the chord of contact of tangents from P ($x_1$​, $y_1$​) to the circle is given by the following:
$x{{x}_{1}}+y{{y}_{1}}={{b}^{2}}$ …(2)
Now, we are given that this chord of contact touches the circle ${{x}^{2}}+{{y}^{2}}={{c}^{2}}$.
So, the length of perpendicular from centre (0, 0) to the chord of contact $x{{x}_{1}}+y{{y}_{1}}={{b}^{2}}$ should be equal to the radius c.
The length perpendicular from a point (p, q) to a line lx + my + n = 0 is given by $\dfrac{|lp+mq+n|}{\sqrt{{{l}^{2}}+{{m}^{2}}}}$
Using this, we will get the following:
$\dfrac{{{b}^{2}}}{\sqrt{{{x}_{1}}^{2}+{{y}_{1}}^{2}}}=c$
Substituting (1) to the above equation, we will get the following:
$\dfrac{{{b}^{2}}}{\sqrt{{{a}^{2}}}}=c$
${{b}^{2}}=ac$
So, a,b, and c are in GP.
Hence, option (b) is correct.

Note: In this question, it is very important to know the formula for the length of perpendicular from a point to a line. The length perpendicular from a point (p, q) to a line lx + my + n = 0 is given by $\dfrac{|lp+mq+p|}{\sqrt{{{l}^{2}}+{{m}^{2}}}}$. Using this formula, you will be able to make the calculation much quicker instead of calculating using basic geometric formulae which will take a lot of time.