Solveeit Logo
Login

Question

Question: If the chord joining the points \(\left( at_{1}^{2},2a{{t}_{1}} \right)\) and \(P\left( at_{2}^{2},2...

If the chord joining the points (at12,2at1)\left( at_{1}^{2},2a{{t}_{1}} \right) and P(at22,2at2)P\left( at_{2}^{2},2a{{t}_{2}} \right) of the parabola y2=4ax{{y}^{2}}=4ax passes through the focus of the parabola, then
A.t1t2=−1{{t}_{1}}{{t}_{2}}=-1
B.t1t2=1{{t}_{1}}{{t}_{2}}=1
C.t1+t2=−1{{t}_{1}}+{{t}_{2}}=-1
D.t1−t2=1{{t}_{1}}-{{t}_{2}}=1

Explanation

Solution

Hint: Take P and Q as the coordinates of the focal chord. S(a,o)S\left( a,o \right) will be the focus. Thus PS and SQ has the same slope. Find the slope of PS and QS separately and equate them to get the relation between t1{{t}_{1}} and t2{{t}_{2}} .

Complete step-by-step answer:
The cord of the parabola which passes through the focus is called the focal chord. Now we have been given the general equation of parabola as y2=4ax{{y}^{2}}=4ax .

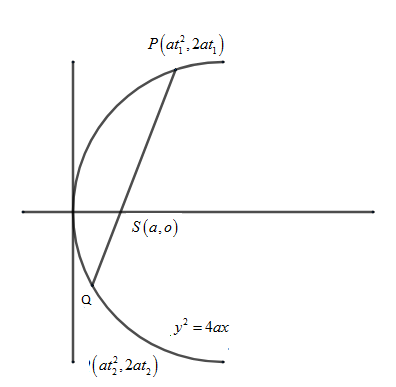
Let us take the points on the parabola as P(at12,2at1)P\left( at_{1}^{2},2a{{t}_{1}} \right) and Q(at22,2at2)Q\left( at_{2}^{2},2a{{t}_{2}} \right) .Any chord to y2=4ax{{y}^{2}}=4ax which para through the focus is called focal chord on the parabola y2=4ax{{y}^{2}}=4ax.
We said that P(at12,2at1)P\left( at_{1}^{2},2a{{t}_{1}} \right) .The coordinate of the other extreme Q of the focal chord is through P is (at22,2at2)\left( at_{2}^{2},2a{{t}_{2}} \right) .Then PS and SQ , where S(a,o)S\left( a,o \right) is the focus has the same slope.
I.e. slope of PS = Slope of QS.
We know the formula of slope as y2−y1x2−x1\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}
Let us first find the slope of PS. Take (x1,y1)=(a,o)\left( {{x}_{1}},{{y}_{1}} \right)=\left( a,o \right) and x2,y2=(at12,2at1){{x}_{2}},{{y}_{2}}=\left( at_{1}^{2},2a{{t}_{1}} \right)
Slope of PS =2at1−0at12−a=2at1a(t12−1)=2t1t12−1=\dfrac{2a{{t}_{1}}-0}{at_{1}^{2}-a}=\dfrac{2a{{t}_{1}}}{a\left( t_{1}^{2}-1 \right)}=\dfrac{2{{t}_{1}}}{t_{1}^{2}-1}
∴\therefore slope of QS =2t2t22−1=\dfrac{2{{t}_{2}}}{t_{2}^{2}-1} .
Now let us equate both the slopes,
Slope of PS = Slope of QS
2t1t12−1=2t2t22−1\dfrac{2{{t}_{1}}}{t_{1}^{2}-1}=\dfrac{2{{t}_{2}}}{t_{2}^{2}-1} can 2 from each side and cross multiply.
∴t1(t22−1)=t2(t12−1) t1t22−t1=t2t12−t2 ⇒t1t22−t2t12−t1+t2=0 t1t2(t2−t1)+(t2−t1)=0 ⇒(t1.t2+1)(t2−t1)=0 \begin{aligned} & \therefore {{t}_{1}}\left( t_{2}^{2}-1 \right)={{t}_{2}}\left( t_{1}^{2}-1 \right) \\\ & {{t}_{1}}t_{2}^{2}-{{t}_{1}}={{t}_{2}}t_{1}^{2}-{{t}_{2}} \\\ & \Rightarrow {{t}_{1}}t_{2}^{2}-{{t}_{2}}t_{1}^{2}-{{t}_{1}}+{{t}_{2}}=0 \\\ & {{t}_{1}}{{t}_{2}}\left( {{t}_{2}}-{{t}_{1}} \right)+\left( {{t}_{2}}-{{t}_{1}} \right)=0 \\\ & \Rightarrow \left( {{t}_{1}}.{{t}_{2}}+1 \right)\left( {{t}_{2}}-{{t}_{1}} \right)=0 \\\ \end{aligned}
Thus from the above equation we can take, t1.t2+1=0{{t}_{1}}.{{t}_{2}}+1=0
∴t1t2=−1\therefore {{t}_{1}}{{t}_{2}}=-1 i.e. t2=−1t1{{t}_{2}}=\dfrac{-1}{{{t}_{1}}} , the point is at Q(at2,−2at)Q\left( \dfrac{a}{{{t}_{2}}},-\dfrac{2a}{t} \right)
Thus we got the four of the parabola t1t2=−1{{t}_{1}}{{t}_{2}}=-1 .
∴\therefore option (A) is the correct answer.
Note: One of the basic identities of the parabola is that if t1{{t}_{1}} and t2{{t}_{2}} are the endpoints of a focal chord. Then their slopes can be connected, so that we get t1t2=−1{{t}_{1}}{{t}_{2}}=-1 . We can answer this question even without the complete solution.