Question

If the centroid of the triangle formed by the points $\left( {0,0} \right)$, $\left( {\cos \theta ,\sin \theta } \right)$ and $\left( {\sin \theta , - \cos \theta } \right)$ lies on the line $y = 2x$ , then $\theta$ is equal to
A.${\tan ^{ - 1}}2$
B.${\tan ^{ - 1}}3$
C.${\tan ^{ - 1}}\left( { - 3} \right)$
D.${\tan ^{ - 1}}\left( { - 2} \right)$

Answer 1

Here we are given that the centroid is formed by the points $\left( {0,0} \right)$, $\left( {\cos \theta ,\sin \theta } \right)$ and $\left( {\sin \theta , - \cos \theta } \right)$
So, we need to apply these vertices in the formula to find the centroid. Then it is given that the centroid lies on the line $y = 2x$. Thus, we shall apply the x-coordinate and the y-coordinate of the centroid on the line and we need to simplify the obtained equation to find the desired answer.
Formula to be used:
a) The formula to calculate the centroid of a given triangle is as follows.
$c = \left( {\dfrac{{{x_1} + {x_2} + {x_3}}}{3},\dfrac{{{y_1} + {y_2} + {y_3}}}{3}} \right)$
Here $c$ is the centroid of the triangle; ${x_1}$ , ${x_2}$ and ${x_3}$ are the x-coordinates of the given three vertices and ${y_1}$ , ${y_2}$ and ${y_3}$ are the y-coordinates of the three vertices.
b) $\dfrac{{\sin \theta }}{{\cos \theta }} = \tan \theta$

Complete answer:

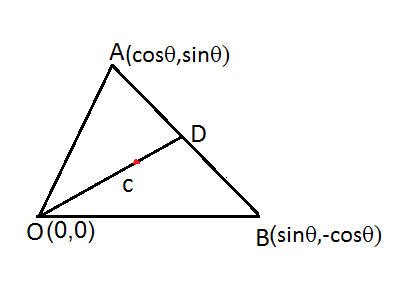
We are given that the centroid of the triangle formed by the points $\left( {0,0} \right)$, $\left( {\cos \theta ,\sin \theta } \right)$ and $\left( {\sin \theta , - \cos \theta } \right)$
We need to calculate the angle.
Thus, the given three vertices are $\left( {0,0} \right)$, $\left( {\cos \theta ,\sin \theta } \right)$ and $\left( {\sin \theta , - \cos \theta } \right)$
We all know that the centroid of the triangle is $c = \left( {\dfrac{{{x_1} + {x_2} + {x_3}}}{3},\dfrac{{{y_1} + {y_2} + {y_3}}}{3}} \right)$
Now, we need to apply the x-coordinates and the y-coordinates of the three vertices in the above formula.
Thus, we get $c = \left( {\dfrac{{0 + \cos \theta + \sin \theta }}{3},\dfrac{{0 + \sin \theta - \cos \theta }}{3}} \right)$
$\Rightarrow c = \left( {\dfrac{{\cos \theta + \sin \theta }}{3},\dfrac{{\sin \theta - \cos \theta }}{3}} \right)$
Thus, we have x-coordinate as $\dfrac{{\cos \theta + \sin \theta }}{3}$ and y-coordinate as $\dfrac{{\sin \theta - \cos \theta }}{3}$
Also, we are given that the centroid of the triangle lies on the line $y = 2x$
So, we need to apply $x = \dfrac{{\cos \theta + \sin \theta }}{3}$ and $y = \dfrac{{\sin \theta - \cos \theta }}{3}$ on the line $y = 2x$
Thus, we have $\dfrac{{\sin \theta - \cos \theta }}{3} = 2\dfrac{{\cos \theta + \sin \theta }}{3}$
Now, we need to simplify the above equation to find the angle.
Hence, $\sin \theta - \cos \theta = 2\cos \theta + 2\sin \theta$
$\Rightarrow \sin \theta - 2\sin \theta = 2\cos \theta + \cos \theta$
$\Rightarrow - \sin \theta = 3\cos \theta$
$\Rightarrow - 3 = \dfrac{{\sin \theta }}{{\cos \theta }}$
$\Rightarrow - 3 = \tan \theta$ (Here we applied $\dfrac{{\sin \theta }}{{\cos \theta }} = \tan \theta$ )
$\Rightarrow \theta = {\tan ^{ - 1}}\left( { - 3} \right)$

Therefore, we found that $\theta = {\tan ^{ - 1}}\left( { - 3} \right)$ and option C) is the answer.

Note:
The centroid is the center point of a triangle and we can also say that the centroid is the point of intersection of three medians of the triangle where median is a line segment that joins a vertex to the midpoint of the opposite side. Also, the centroid is formed by the three vertices of the triangle.