Question

If the centroid of tetrahedron OABC where A, B, C are given by (a, 2, 3), (1, b, 2) and (2, 1, c) respectively is (1, 2, -2), then distance of P (a, b, c) from origin is
a) $\sqrt{195}$
b) $\sqrt{14}$
c) $\sqrt{\dfrac{107}{14}}$
d) $\sqrt{13}$

Answer 1

The centroid or geometric center of a figure is the arithmetic mean position of all the points in the figure. Let ABCD is a tetrahedron whose vertices $\text{A(}{{\text{x}}_{1}}\text{,}{{\text{y}}_{1}}\text{,}{{\text{z}}_{1}}\text{); B(}{{\text{x}}_{2}}\text{,}{{\text{y}}_{2}}\text{,}{{\text{z}}_{2}}\text{); C(}{{\text{x}}_{3}}\text{,}{{\text{y}}_{3}}\text{,}{{\text{z}}_{3}}\text{)}$ and $\text{D(}{{\text{x}}_{4}}\text{,}{{\text{y}}_{4}}\text{,}{{\text{z}}_{4}}\text{)}$then, the centroid (G) is given as:
$G(x,y,z)=\left[ \dfrac{{{x}_{1}}+{{x}_{2}}+{{x}_{3}}+{{x}_{4}}}{4},\dfrac{{{y}_{1}}+{{y}_{2}}+{{y}_{3}}+{{y}_{4}}}{4},\dfrac{{{z}_{1}}+{{z}_{2}}+{{z}_{3}}+{{z}_{4}}}{4} \right]$. Use this formula to find the centroid for triangle OABC and then equate the coordinates with the point (1, 2, -2) to get the values of a, b and c. Now, we get point P (a, b, c). Then, find the distance between point origin and point P (a, b, c) using distance formula:
$d=\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}+{{\left( {{z}_{2}}-{{z}_{1}} \right)}^{2}}}$

Complete step by step answer:
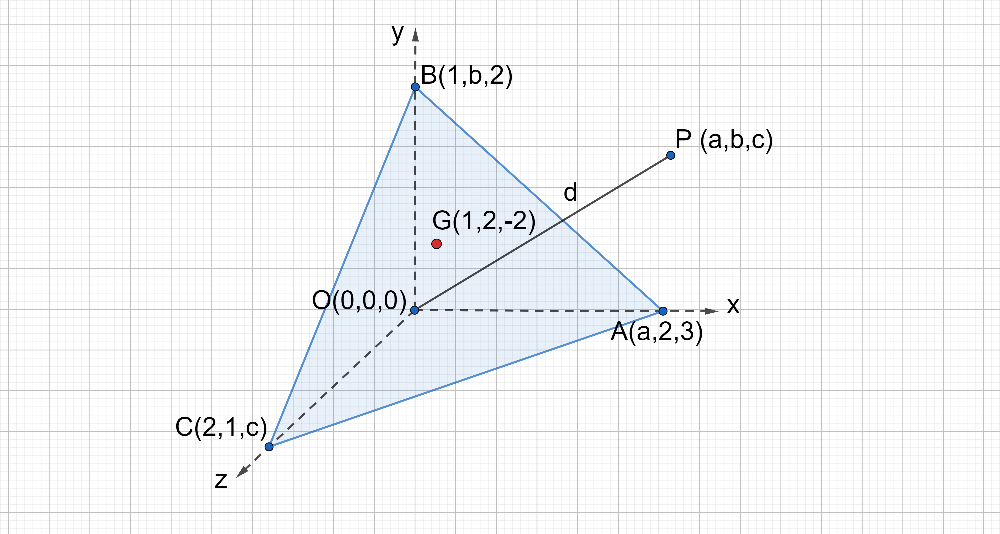
Consider the diagram of tetrahedron OABC given below, whose vertices are $\text{A(a,2,3);B(1,b,2);C(2,1,c)}$ and $\text{O(0,0,0)}$.
G (1, 2, -2) represents the centroid of the tetrahedron, and P (a, b, c) is the arbitrary point at a distance ‘d’ from the origin.

For a tetrahedron with vertices, $\text{A(}{{\text{x}}_{1}}\text{,}{{\text{y}}_{1}}\text{,}{{\text{z}}_{1}}\text{); B(}{{\text{x}}_{2}}\text{,}{{\text{y}}_{2}}\text{,}{{\text{z}}_{2}}\text{); C(}{{\text{x}}_{3}}\text{,}{{\text{y}}_{3}}\text{,}{{\text{z}}_{3}}\text{)}$ and $\text{D(}{{\text{x}}_{4}}\text{,}{{\text{y}}_{4}}\text{,}{{\text{z}}_{4}}\text{)}$, the centroid (G) is given as:
$G(x,y,z)=\left[ \dfrac{{{x}_{1}}+{{x}_{2}}+{{x}_{3}}+{{x}_{4}}}{4},\dfrac{{{y}_{1}}+{{y}_{2}}+{{y}_{3}}+{{y}_{4}}}{4},\dfrac{{{z}_{1}}+{{z}_{2}}+{{z}_{3}}+{{z}_{4}}}{4} \right]$
Therefore, for the given tetrahedron OABC whose vertices are $\text{A(a,2,3);B(1,b,2);C(2,1,c)}$ and $\text{O(0,0,0)}$, the centroid is
$\text{G}(1,2,-2)=\left[ \dfrac{\text{a}+1+2+0}{4},\dfrac{2+\text{b}+1+0}{4},\dfrac{3+2+\text{c}+0}{4} \right]......(1)$
By equating the coordinates of centroid in equation (1), we get:

& \dfrac{3+a}{4}=1......(2) \\\ & \dfrac{b+3}{4}=2......(3) \\\ & \dfrac{5+c}{4}=-2.......(4) \\\ \end{aligned}$$ So, we get values of a, b and c from equation (2), (3) and (4); $$\begin{aligned} & \Rightarrow a=1 \\\ & \Rightarrow b=5 \\\ & \Rightarrow c=-13 \\\ \end{aligned}$$ Since the arbitrary point P is given as P (a, b, c). Substituting values of a, b, and c, we can write it as: P (1, 5, -13) Now, we need to find the distance between P (1, 5, -13) and origin O (0, 0, 0). To find distance between two points $$\text{P(}{{\text{x}}_{1}}\text{,}{{\text{y}}_{1}}\text{,}{{\text{z}}_{1}}\text{) and Q(}{{\text{x}}_{2}}\text{,}{{\text{y}}_{2}}\text{,}{{\text{z}}_{2}}\text{)}$$, use distance formula, i.e. $$d=\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}+{{\left( {{z}_{2}}-{{z}_{1}} \right)}^{2}}}$$ Therefore, distance between P (1, 5, -13) and origin O (0, 0, 0) is: $$\begin{aligned} & d=\sqrt{{{\left( 1-0 \right)}^{2}}+{{\left( 5-0 \right)}^{2}}+{{\left( -13-0 \right)}^{2}}} \\\ & =\sqrt{1+25+169} \\\ & =\sqrt{195} \end{aligned}$$ **So, the correct answer is “Option A”.** **Note:** Another way to find centroid is stated below: Firstly, find the centroids of each of the triangular faces of the tetrahedron. All the centroids when joined together form a triangle itself. Find the centroid of that triangle, which is the centroid of the tetrahedron. Equate the coordinates and get the values of a, b and c. Hence, find the distance between origin and P (a, b, c).