Question

If the center of square ABCD is at $z=0$. If affix of vertex $A\text{ is }{{z}_{1}}$, centroid of triangle ABC is/are

& A.\dfrac{{{z}_{1}}}{3}\left( \cos \pi +i\sin \pi \right) \\\ & B.4\left[ \left( \cos \dfrac{\pi }{2} \right)-i\left( \sin \dfrac{\pi }{2} \right) \right] \\\ & C.\dfrac{{{z}_{1}}}{3}\left[ \left( \cos \dfrac{\pi }{2} \right)+i\left( \sin \dfrac{\pi }{2} \right) \right] \\\ & D.\dfrac{{{z}_{1}}}{3}\left[ \left( \cos \dfrac{\pi }{2} \right)-i\left( \sin \dfrac{\pi }{2} \right) \right] \\\ \end{aligned}$$

Answer 1

Hint : First we find the affix of vertex C by using the midpoint concept in terms of ${{z}_{1}}$. Next we find the affix of vertex B by using the rotation concept. If $z$ is formed by rotating $x$ by angle of $\theta$ we write $x{{e}^{i\theta }}=z$ where ${{e}^{i\theta }}$ by Euler’s formula is equal to ${{e}^{i\theta }}=\cos \theta +i\sin \theta$. We find the affix of centroid using affixes of the three vertices of triangle ABC. $$$$
Complete step-by-step answer :
Given condition about the center of the square in the question is written:
$center=z=0$
We are given in the question that affix of A is ${{z}_{1}}$ which means
$A={{z}_{1}}$
We denote the affixes of $B,C$ as ${{z}_{3}},{{z}_{2}}$. The center O’ is the midpoint of points A, C. Because in squares the diagonals intersect at the center and bisect each other. By using mid-point theory we can say that the affix of O’ is the average of affixes of A, C.

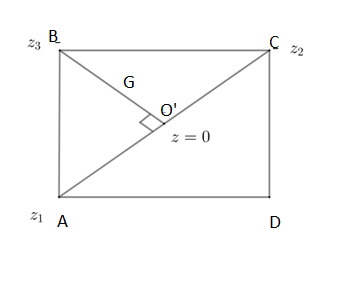
By substituting values we get it as follows:
$O'=\dfrac{A+C}{2}$
By substituting points, we can write the equation as:
$z=0=\dfrac{{{z}_{1}}+{{z}_{2}}}{2}$
By multiplying 2 on both sides, we get the equation:
${{z}_{1}}+{{z}_{2}}=0$
By subtracting ${{z}_{1}}$ on both sides, we get it as:
${{z}_{1}}+{{z}_{2}}-{{z}_{1}}=0-{{z}_{1}}$
By simplifying the above equation, we can say the affix of C is:
${{z}_{2}}=-{{z}_{1}}\ldots \ldots \ldots \ldots ..\left( \text{1} \right)$
As the diagonals bisect each other and are of equal length. The triangle AO’B is isosceles. By this, we can say O’AD is also isosceles. So, we say diagonals bisect the angles. By this, we get that
$\angle O'AB = \angle ABO'={{45}^{\circ }}$
So, the sum of angles in the triangle is ${{180}^{\circ }}=\pi.$ By this we get angle AO’B $= {{90}^{\circ }}=\dfrac{\pi }{2}$.
So, rotating ${{z}_{1}}\text{ by 9}{{\text{0}}^{\circ }}$ we get ${{z}_{3}}$. By angle theorem if we get z by rotating $x$ b $\theta$ we say:
$x{{e}^{i\theta }}=z\,\,\Rightarrow \,\,x\left( \cos \theta +i\sin \theta \right)=z$
We have to rotate ${{z}_{1}}$ the affix of A by ${{90}^{\circ }}=\dfrac{\pi }{2}$ to have,
${{z}_{3}}={{z}_{1}}\left( \cos \dfrac{\pi }{2}+i\sin \dfrac{\pi }{2} \right)......\left( 2 \right)$
So we have obtained the affixes of $A,B,C$ in terms of ${{z}_{1}}$. So the affix of centroid G is
$G=\dfrac{{{z}_{1}}+{{z}_{2}}+{{z}_{3}}}{3}$
By substituting their values in terms of $z$ from (1) and (2), we get equation:
$\text{G}=\dfrac{{{z}_{1}}-{{z}_{1}}+{{z}_{1}}\left( \cos \dfrac{\pi }{2}+i\sin \dfrac{\pi }{2} \right)}{3}$
By simplifying, we get centroid
$\Rightarrow \dfrac{{{z}_{1}}}{3}\left( \cos \dfrac{\pi }{2}+i\sin \dfrac{\pi }{2} \right)$
We can also take $\theta =-\dfrac{\pi }{2}$ with respect to $OA$ and rotate to B to get the centroid as
$G=\dfrac{{{z}_{1}}}{3}\left( \cos \dfrac{\pi }{2}-i\sin \dfrac{\pi }{2} \right)$
Therefore, option (c) and (d) are correct.

Note : We have to be careful while taking the mid-point theory because we must not confuse and add $\dfrac{{{z}_{1}}+{{z}_{2}}}{2}$ not $\dfrac{{{z}_{1}}+0}{2}={{z}_{2}}$. While applying angle rotating concept ${{e}^{i\theta }}$ must be multiplied to the original vector, not the resultant vector. We can alternatively find the centroid using the section formula with affixes of B and O’ with a ratio of 2:1.