Question

If the area of the triangle whose one vertex is at the vertex of the parabola, ${{y}^{2}}+4\left( x-{{a}^{2}} \right)=0$ and the other two vertices are the points on intersection on the parabola and $y$ - axis is 250sq. units , then value of $''a''$ is:
(a) $5\sqrt{5}$
(b) ${{10}^{\dfrac{2}{3}}}$
(c) $5\left( {{2}^{\dfrac{1}{3}}} \right)$
(d) $5$

Answer 1

Draw the graph of the given triangle and through the graph, guess the base and height of the triangle, which are going to come in terms of $''a''$. Once you know the base and height put them to the formula of area of triangle i.e.
Area = $\dfrac{1}{2}\times b\times h$ ; $b$ is the base and $h$ is the height and solve for $''a''$

Complete step-by-step answer:
First , we will draw the graph of the triangle and the given parabola

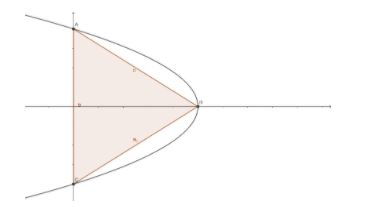
As we can see that one vertex of the triangle is at the vertex of parabola which is $\left( {{a}^{2}},0 \right)$
We can observe from the graph that $OB$ is the height of this triangle which is equal to ${{a}^{2}}$
Now, we will find the base of the triangle,
We can observe from the graph that $AC$ is the base of the triangle
We can find $A$ and $C$ by putting $x=0$ , in the equation of parabola,
$\begin{aligned} & {{y}^{2}}+4\left( x-{{a}^{2}} \right)=0 \\\ & {{y}^{2}}+4\left( 0-{{a}^{2}} \right)=0 \\\ & {{y}^{2}}=4{{a}^{2}} \\\ & y=\pm 2a \end{aligned}$
Hence, $\begin{aligned} & A=\left( 0,2a \right) \\\ & C=\left( 0,-2a \right) \\\ \end{aligned}$
Hence, the value of $AC=4a$
Now, we have the base , height and area of the triangle , we can put these values to the formula of area of triangle and get the value of $''a''$
We know that Area of triangle = $\dfrac{1}{2}\times b\times h$
Applying this formula and putting the known values to it , we get,
$\begin{aligned} & 250=\dfrac{1}{2}\times 4a\times {{a}^{2}} \\\ & 250=2{{a}^{3}} \\\ & {{a}^{3}}=125 \\\ & a=5 \end{aligned}$
Hence , we get the value of $a=5$

So, the correct answer is “Option d”.

Note: The alternate method for this question is to divide the region into 2 parts , one that is above the $x$ - axis and one below it . As the graph is symmetric about the $x$ - axis , so we can evaluate the area of a region using the method of integration and then multiply it by 2. For that , first we will find the equation of line $AB$ and find the area under that line using the method of integration and then multiply it by 2 and equate that area with 250 and hence get the value of $''a''$ .