Question

If the area of the region bounded by curves, $y = {x^2},y = \dfrac{1}{x}$ and the lines $y = 0$ and $x = t(t > 1)$ is $1$ sq. unit, then $t$ is equal to?
$A)\,\dfrac{4}{3} \\\ B)\,{e^{\dfrac{2}{3}}} \\\ C)\,\dfrac{3}{2} \\\ D)\,{e^{\dfrac{3}{2}}} \\\$

Answer 1

In this question we are given an area of region bounded by some curves and lines. We will firstly draw the graph using given information. Then the area under the curve between two points can be found by doing a definite integral between the two points.

Complete step-by-step answer:
We are given that area of the region bounded by the curves $y = {x^2},y = \dfrac{1}{x}$ and the lines $y = 0$ and $x = t(t > 1)$ is $1$ sq. unit.

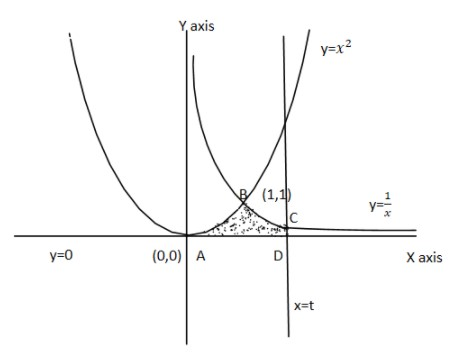
So above is the graph for given information. An area bounded by the given curves is the region ABCD.
Now, we know that the area under a curve between two points can be found by doing a definite integral between the two points. That is, to find the area under the curve $y = f\left( x \right)$ between $x = a\,\&\, x = b$ is
Area under $y = f(x) = \int_a^b {f(x)dx} \,\,\,\,\,\,\,\,\,\,\, \to \left( 1 \right)$
Now from the graph we can say that
Area under region ABCD$=$ Area under curve AB + Area under curve BC $\to \left( 2 \right)$
Now firstly we will consider area under curve AB
We know curve AB is $y = {x^2}$ between $x = 0\,\& \,x = 1$
Now substituting $a = 0\,,\,b = 1\,,\,y = f(x) = {x^2}$ in (1) , the area under AB will be
Area under AB$= \int\limits_0^1 {{x^2}} dx$
Now we know that $\int {{x^n}dx} = \dfrac{{{x^{n + 1}}}}{{n + 1}} + c$ , so area under curve AB is
$= \left[ {\dfrac{{{x^{2 + 1}}}}{{2 + 1}}} \right]_0^1 \\\ = \left[ {\dfrac{{{x^3}}}{3}} \right]_0^1 \\\ = \dfrac{{{1^3}}}{3} - 0 \\\ = \dfrac{1}{3}\,\,$
So area under AB$= \dfrac{1}{3}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \to \left( 3 \right)$
Now we will consider curve BC
Now we know that BC is $y = \dfrac{1}{x}$ between $x = 1\,\&\, x = t$
Now again substituting $a = 1\,,\,b = t\,,\,y = f(x) = \dfrac{1}{x}$ in (1), the area of BC becomes,
Area under BC$= \int\limits_1^t {\dfrac{1}{x}} dx$
Now we know $\int {\dfrac{1}{x}dx = \ln x + c}$ , so area under curve BC
$= \left[ {\ln x} \right]_1^t \\\ = \ln t - \ln 1 \\\ = \ln t \\\$
So we get area under curve BC$= \ln t\,\,\,\,\,\,\,\,\,\,\,\,\, \to \left( 4 \right)$
Now substituting values area under curve AB and BC from (3) and (4) in (2) we get
Area under region ABCD$= \dfrac{1}{3} + \ln t\,\,\,\,\,\,\,\,\,\,\,\,\,\, \to \left( 5 \right)$
Now according to the question we know that the area enclosed by the given curves and lines is one sq. unit i.e. the area enclosed by region ABCD is one sq. unit.
Area under region ABCD$= 1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \to \left( 6 \right)$
Now from equation (5) and (6) we get
$1 = \dfrac{1}{3} + \ln t\, \\\ \ln t = 1 - \dfrac{1}{3} \\\ \ln t = \dfrac{2}{3} \\\$
Now taking exponential on both sides
${e^{\ln t}} = {e^{\dfrac{2}{3}}} \\\ t = {e^{\dfrac{2}{3}}}$
Hence value of $t$ is ${e^{\dfrac{2}{3}}}$

So, the correct answer is “Option B”.

Note: The important part in the question is to make the graph using the given information. And to make the graph we will first take the equation $y = {x^2}$ , we know it represents parabola with vertex at origin.Now next is $y = \dfrac{1}{x}$ which is a reciprocal function and its graph form a rectangular hyperbola.Now we can easily find the intersection point of both curves that is $\left( {1,1} \right)$.Next is the line $y = 0$ which is $x$ axis.Then we have $x = t(t > 1)$so we can locate it easily because $t > 1$ . so it will lie after the intersection of both the curves.Now by just locating these points on a graph we can see the area bounded by these curves and lines.