Question

If the area (in square units) bounded by the parabola ${{y}^{2}}=4\lambda x$ and the line $y=\lambda x,\lambda >0$, is $\dfrac{1}{9}$, then $\lambda$ is equal to $A.24$
B.48$$$$
C.4\sqrt{3}$$$$$ D. 2\sqrt{6}$$$$$

Answer 1

Put the value of $y=\lambda x$ from the equation of the line in the equation of parabola ${{y}^{2}}=4\lambda x$ to find the points of intersection of the line and the parabola. Use definite integral with abscissas of the intersection of the point as limits to find the area under the parabola and line. Equate their difference to $\dfrac{1}{9}$ and find the only unknown $\lambda$ .$$$$

Complete step-by-step answer :

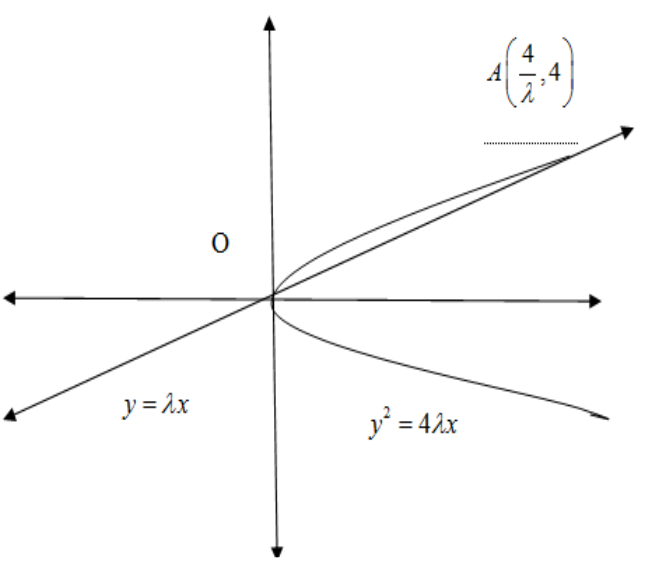
The given equation of parabola is
${{y}^{2}}=4\lambda x...(1)$
Where $\lambda$ is a positive real number. The given equation of line
$y=\lambda x...(2)$
We solve the pair of equations by putting the values of $y$ in equation(1),

& {{\left( \lambda x \right)}^{2}}=4\lambda x \\\ & \Rightarrow {{\lambda }^{2}}{{x}^{2}}=4\lambda x \\\ & \Rightarrow x\left( {{\lambda }^{2}}x-4\lambda \right)=0 \\\ & \Rightarrow x=0,\dfrac{4}{\lambda } \\\ \end{aligned}$$ When $x=0,y=0$ and one of the points of intersection of parabola and the line is origin. The other point of intersection is given by $x=\dfrac{4}{\lambda },y= \lambda \left( \dfrac{4}{\lambda } \right)=4$. Here, $\dfrac{4}{\lambda }$ exists as $\lambda $ is real and positive number. So the area bounded by the parabola and the line has points $\left( 0,0 \right)$ and $\left( \dfrac{4}{\lambda },4 \right)$ at the boundary. $$$$ We know from the theory of definite integral that the area under any curve $f\left( x \right)$ within enclosed by vertical lines $x=a,x=b$ is given by $\int\limits_{a}^{b}{f\left( x \right)}dx$. The area under parabola within the points of intersection $\left( 0,0 \right)$and $\left( \dfrac{4}{\lambda },4 \right)$ can be expressed as $\int\limits_{0}^{\dfrac{4}{\lambda }}{\sqrt{4\lambda x}}dx$ and similarly the area under the line can be expressed as $\int\limits_{0}^{\dfrac{4}{\lambda }}{\lambda xdx}$.$$$$ We observe that the area bounded by the parabola and the line is the difference between the area under parabola and the line which is given in the question as 9 square units. We also deduce $\sqrt{4\lambda }>\lambda $ as $\lambda $ is positive. So the line will lie under the parabola within the bounds defined by points of intersection. So $$9=\int\limits_{0}^{\dfrac{4}{\lambda}}{\sqrt{4\lambda x}}dx-\int\limits_{0}^{\dfrac{4}{\lambda }}{\lambda xdx}$$ Using the integration formula $\int{{{x}^{n}}dx}=\dfrac{{{x}^{n}}+1}{n+1}$ we get, $$\begin{aligned} & \dfrac{1}{9}={{\left[ 2\sqrt{\lambda }\cdot \dfrac{2}{3}\cdot {{x}^{\dfrac{3}{2}}}-\lambda \dfrac{{{x}^{2}}}{2} \right]}_{0}}^{\dfrac{4}{\lambda }} \\\ & \Rightarrow \dfrac{1}{9}=\dfrac{4\sqrt{\lambda }}{3}\cdot \dfrac{4}{\lambda }\cdot \dfrac{2}{\sqrt{\lambda }}-\dfrac{\lambda }{2}\cdot \dfrac{16}{{{\lambda }^{2}}} \\\ & \Rightarrow \dfrac{1}{9}=\dfrac{32}{3\lambda }-\dfrac{8}{\lambda } \\\ & \Rightarrow \lambda =24 \\\ \end{aligned}$$ **The correct choice is A.$$$$** **Note** : We need to take care that area is a positive quantity and we need to subtract the smaller area from the larger area. So we need to investigate under which curve more area is bounded. It is also to be noted that if some part of the curve if lies below $x-$axis and some above part above then the formula within interval $\left[ a,b \right]$ then the formula for area $\int\limits_{a}^{b}{f\left( x \right)}dx$ fails there. We have to find the sum of the area below and above the $x-$axis.