Question

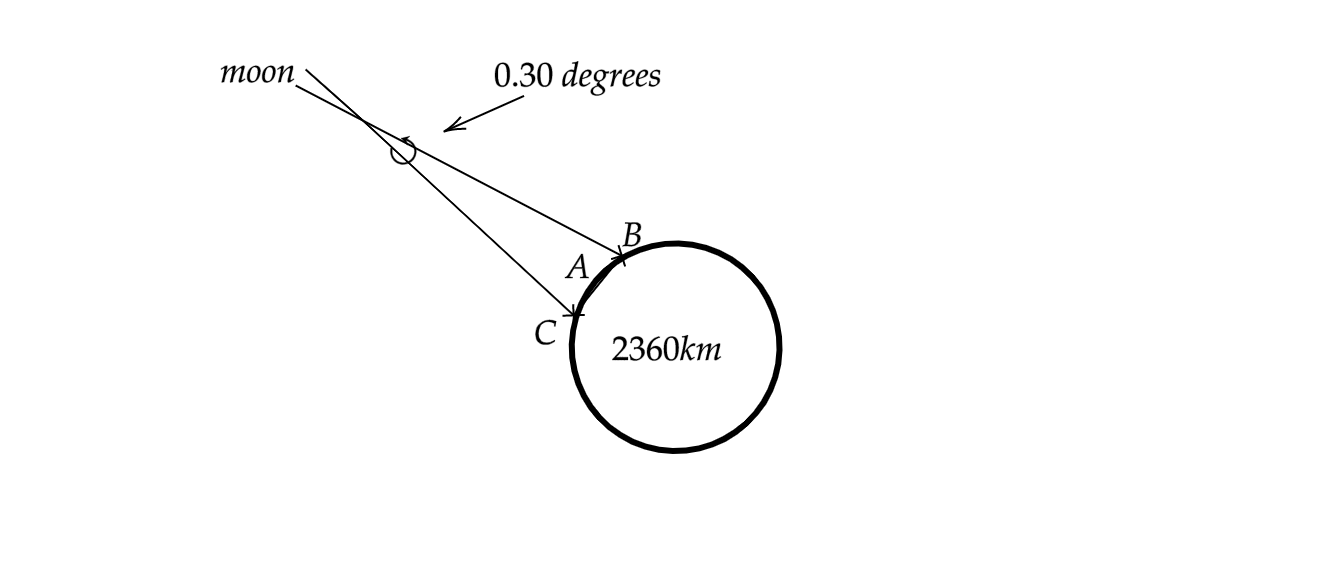
If the angular distance between the stars turns out to be approximately $1100$ arc seconds, or $0.30$ degrees. The moon appears to shift $0.3$ degrees when we observe it from two vantage points $2360km$ apart, then find the distance of the moon from the surface of the earth. Given the angular diameter of the moon is $0.5$ degrees.

A) $450642km$
B) $450392km$
C) $325684km$
D) $480264km$

Answer 1

The phenomenon mentioned in the given question is parallax. Parallax is the apparent angular displacement of a celestial body due to its being observed from the surface of the earth instead of the centre of the earth. Parallax also arises due to a change in viewpoint caused by relative motion.

Complete step by step solution:
From the given question, we can say that the shift in the angular distance of the moon when viewed from two different vantage points is $0.3$ degrees. Let this angular shift be $\theta$.
Since angular measurements are usually made in radians, we must convert the given angular distance into radians.

& \theta =0.3{}^\circ \\\ & \Rightarrow \theta =0.3\times \dfrac{\pi }{180}rad \\\ & \Rightarrow \theta =\dfrac{\pi }{600}rad \\\ \end{aligned}$$ Using the properties of circles and arcs, we can say that arc length in a circle is equal to the product of the radius and the angle subtended by the arc.  Since the distance between the moon and the earth is more than the radius of the earth, the distance between the moon and the earth, DA, is roughly equal to DC. Now for the arc BAC, we can say that arc length will be equal to the product of the radius, DC, and the angle subtended at DC. Mathematically, we can say that $$d=D\times \theta $$ where $$d$$ is the arc length. Substituting the values, we get $$\begin{aligned} & d=D\times \theta \\\ & \Rightarrow 2360=D\times \dfrac{\pi }{600}rad \\\ & \Rightarrow D=\dfrac{2360\times 600}{\pi }=450642km \\\ \end{aligned}$$ **Hence, option (A) is the correct answer.** **Note:** An alternative method to approach this question is using the definition of parallax. The Parallax formula states that the distance to a star is equal to the distance between the vantage points divided by the parallax angle, where the parallax angle is measured in arcseconds.