Question

If the angle subtended by the arc of a sector at the centre is 90 degrees, then the area of the sector in square units is
(a) $2\pi {{r}^{2}}$
(b) $4\pi {{r}^{2}}$
(c) $\dfrac{\pi {{r}^{2}}}{4}$
(d) $\dfrac{\pi {{r}^{2}}}{2}$

Answer 1

Hint: In this question, we first need to find the length of the arc using the formula $l=r\theta$. Then substitute this value of arc length in the area of the sector formula given by $A=\dfrac{1}{2}rl$ and simplify further to get the result.

Complete step-by-step answer:
Now, form the given conditions in the question we have angle subtended at the centre as 90 degrees which gives
$\theta ={{90}^{\circ }}$
Now, this can also be written in the radians as
$\theta =\dfrac{\pi }{2}$
Now, as we already know that in the sector of a circle the length of the arc is given by the formula
$l=r\theta$
Here, l is the length of the arc, r is the radius of the corresponding circle and $\theta$is the angle subtended by the arc at the centre
Now, let us assume that the radius of the circle as r and length of the arc as l
Given in the question that $\theta =\dfrac{\pi }{2}$
Let us draw the diagram with the above given conditions

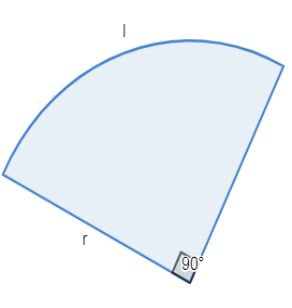
Now, from the length of the arc formula on substituting the respective values we get,
$\Rightarrow l=r\theta$
Now, on further substitution we get,
$\Rightarrow l=\dfrac{\pi r}{2}$
Let us also assume that the area of the circle as A
Now, we can find the area of the sector using the formula
$A=\dfrac{1}{2}rl$
As we already have the value of length of arc from above calculations we get,
$l=\dfrac{\pi r}{2}$
Now, on substituting the respective values in the area of sector formula we get,
$\Rightarrow A=\dfrac{1}{2}\times r\times \dfrac{\pi r}{2}$
Now, on simplifying it further we get,
$\therefore A=\dfrac{\pi {{r}^{2}}}{4}$
Hence, the correct option is (c).

Note:Instead of converting the given angle to radians we can also use the respective formula in terms of degrees and simplify further to get the answer. Both the methods give the same result.It is important to note that finding the length of the arc is not necessary because we can substitute the length formula in the area formula and then directly substitute the angle to get the result.