Question

If the angle of intersection at a point where the two circles with radii 5 cm and 12 cm intersect is ${{90}^{\circ }}$, then the length (in cm) of their common chord is:
(a)$\dfrac{60}{13}$
(b)$\dfrac{120}{13}$
(c)$\dfrac{13}{2}$
(d)$\dfrac{13}{5}$

Answer 1

First of all, draw the figure in which two circles with radii 5 cm and 12 cm intersect is ${{90}^{\circ }}$. Then join the point of intersections with the centre of the circles and also the centres of the two circles. After joining all these points you will have four right angled triangles then using Pythagora's theorem find the length of the common chord. In Pythagoras theorem, ${{\left( Hypotenuse \right)}^{2}}={{\left( Perpendicular \right)}^{2}}+{{\left( Base \right)}^{2}}$.

Complete step-by-step answer :
In the figure, we have drawn two circles with radii 5 cm and 12 cm intersecting each other at points E and F.

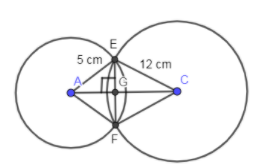
In the above figure, the common chord is represented by EF. Let us assume the length of EG and GF as x.
Also, EF and AC divide the quadrilateral AECF into 4 right triangles so applying the Pythagoras theorem in triangles AGE and CGE we get,
We know that Pythagora's theorem is equal to the square of hypotenuse is equal to the sum of the square of perpendicular and the square of base.
${{\left( Hypotenuse \right)}^{2}}={{\left( Perpendicular \right)}^{2}}+{{\left( Base \right)}^{2}}$
Now, in $\Delta AGE$ we get,
$\begin{aligned} & {{\left( 5 \right)}^{2}}={{\left( x \right)}^{2}}+{{\left( AG \right)}^{2}} \\\ & \Rightarrow {{\left( AG \right)}^{2}}={{\left( 5 \right)}^{2}}-{{\left( x \right)}^{2}} \\\ \end{aligned}$
Taking square root on both the sides we get,
$AG=\sqrt{{{\left( 5 \right)}^{2}}-{{\left( x \right)}^{2}}}$
Now, in $\Delta CGE$ we get,
$\begin{aligned} & {{\left( 12 \right)}^{2}}={{\left( x \right)}^{2}}+{{\left( GC \right)}^{2}} \\\ & \Rightarrow {{\left( GC \right)}^{2}}={{\left( 12 \right)}^{2}}-{{\left( x \right)}^{2}} \\\ \end{aligned}$
Taking square root on both the sides we get,
$GC=\sqrt{{{\left( 12 \right)}^{2}}-{{\left( x \right)}^{2}}}$
Now, it is given in the problem that the circles are intersecting each other at ${{90}^{\circ }}$ means $\Delta AEC$ is right angled at E so applying Pythagoras theorem in that triangle we get,
$\begin{aligned} & {{\left( AC \right)}^{2}}={{\left( AE \right)}^{2}}+{{\left( EC \right)}^{2}} \\\ & \Rightarrow {{\left( AC \right)}^{2}}={{\left( 5 \right)}^{2}}+{{\left( 12 \right)}^{2}} \\\ & \Rightarrow {{\left( AC \right)}^{2}}=25+144 \\\ & \Rightarrow {{\left( AC \right)}^{2}}=169 \\\ \end{aligned}$
Taking square root on both the sides we get,
$AC=13$
Now, the length of AC is equal to the length of AG and GC which you can see from the figure.

$AG+GC=AC$
Substituting the above lengths from the above we get,
$\begin{aligned} & AG+GC=AC \\\ & \Rightarrow \sqrt{{{\left( 5 \right)}^{2}}-{{\left( x \right)}^{2}}}+\sqrt{{{\left( 12 \right)}^{2}}-{{\left( x \right)}^{2}}}=13 \\\ & \Rightarrow \sqrt{{{\left( 5 \right)}^{2}}-{{\left( x \right)}^{2}}}=13-\sqrt{{{\left( 12 \right)}^{2}}-{{\left( x \right)}^{2}}} \\\ \end{aligned}$
Squaring both the sides we get,
$\left( {{\left( 5 \right)}^{2}}-{{\left( x \right)}^{2}} \right)=169+144-{{x}^{2}}-2.13\left( \sqrt{144-{{x}^{2}}} \right)$
${{x}^{2}}$ will be cancelled from both the sides we get,
$\begin{aligned} & 25=169+144-26\left( \sqrt{144-{{x}^{2}}} \right) \\\ & \Rightarrow 26\left( \sqrt{144-{{x}^{2}}} \right)=288 \\\ \end{aligned}$
Dividing 26 on both the sides we get,
$\begin{aligned} & \left( \sqrt{144-{{x}^{2}}} \right)=\dfrac{288}{26} \\\ & \Rightarrow \left( \sqrt{144-{{x}^{2}}} \right)=\dfrac{144}{13} \\\ \end{aligned}$
Taking square on both the sides we get,

& 144-{{x}^{2}}=\dfrac{{{\left( 144 \right)}^{2}}}{{{\left( 13 \right)}^{2}}} \\\ & \Rightarrow 144-\dfrac{{{\left( 144 \right)}^{2}}}{{{\left( 13 \right)}^{2}}}={{x}^{2}} \\\ \end{aligned}$$ $$\begin{aligned} & \Rightarrow \dfrac{\left( 144 \right){{\left( 13 \right)}^{2}}-{{\left( 144 \right)}^{2}}}{{{\left( 13 \right)}^{2}}}={{x}^{2}} \\\ & \Rightarrow \dfrac{24336-20736}{{{\left( 13 \right)}^{2}}}={{x}^{2}} \\\ & \Rightarrow \dfrac{3600}{{{\left( 13 \right)}^{2}}}={{x}^{2}} \\\ \end{aligned}$$ Taking square root on both the sides we get, $x=\dfrac{60}{13}cm$ Now, the length of the common chord is 2x so multiplying x by 2 we get, $2x=\dfrac{120}{13}cm$ Hence, the correct option is (b). **Note** : The mistake that could happen in this problem is that after getting the value of x, students forget to double it because the length of the common chord is twice of x. And you cannot even notice your mistake because in the options this value of x i.e. $\dfrac{60}{13}$ is given so you very delightfully mark the option (a). This is the trap that the examiner set in the objective exam so make sure you won’t repeat this mistake.