Question

If the angle of a prism is ${{60}^{0}}$ and angle of minimum deviation is ${{40}^{0}}$, then the angle of refraction in the prism will be –

& \text{A) 3}{{\text{0}}^{0}} \\\ & \text{B) 4}{{\text{5}}^{0}} \\\ & \text{C) 5}{{\text{0}}^{0}} \\\ & \text{D) 2}{{\text{0}}^{0}} \\\ \end{aligned}$$

Answer 1

We need to understand the relation between the angle of a prism, the angle of minimum deviation and the refracting angles to find the solution to our problem. The refraction through the prism has various relations with its parameters.

Complete step by step solution:
We are given the angle measures of the prism and the minimum deviation for a light through the same. We need to find the refracting angle in such a condition when the minimum deviation is attained. Consider the given figure, where A is the angle of the prism, r’ is the angle of minimum deviation, i is the incident angle, e is the emergence angle and ${{\text{r}}_{\text{1}}}\text{ and }{{\text{r}}_{\text{2}}}$are the refracted angles in the prism.

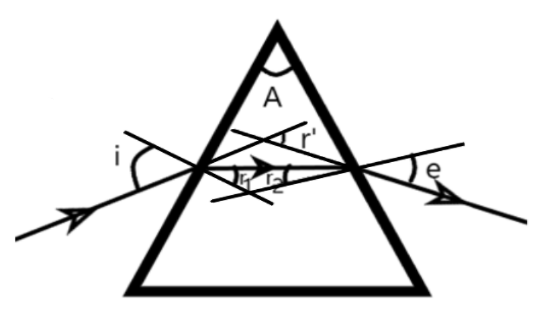
We know that at the condition when the minimum deviation condition is attained, the ray through the prism will be parallel to the base of the prism. Also, the refraction angle ${{\text{r}}_{\text{1}}}\text{ and }{{\text{r}}_{\text{2}}}$will be equal. The angle of incidence and the emergence angles are also equal.
We can understand that the refraction angles of the prism will be half the angle of the prism in this condition.

& {{r}_{1}}={{r}_{2}}=r \\\ & i=e \\\ \end{aligned}$$ We get that from the exterior angle property of triangles as – $$\begin{aligned} & 180-2r=180-A \\\ & \therefore r=\dfrac{A}{2} \\\ \end{aligned}$$ So, the angle of refraction for a prism whose angle is $${{60}^{0}}$$, when the light ray has the minimum deviation through the prism is given as – $$\begin{aligned} & r=\dfrac{A}{2} \\\ & \therefore r=\dfrac{{{60}^{0}}}{2}={{30}^{0}} \\\ \end{aligned}$$ The required angle of refraction is $${{30}^{0}}$$. **The correct answer is option A.** **Note:** The relation between the angle of prism and the angle of refraction can be derived from very simple calculations involving the exterior angle properties of the triangle and the angle sum property of the triangle including these angles in appropriate triangles.