Solveeit Logo
Login

Question

Question: If the angle \(\angle A={{90}^{\circ }}\) in the \(\Delta ABC\), then \[{{\tan }^{-1}}\left( \dfrac{...

If the angle ∠A=90∘\angle A={{90}^{\circ }} in the ΔABC\Delta ABC, then tan⁡−1(ca+b)+tan⁡−1(ba+c){{\tan }^{-1}}\left( \dfrac{c}{a+b} \right)+{{\tan }^{-1}}\left( \dfrac{b}{a+c} \right) is
A. 0
B. 1
C. π4\dfrac{\pi }{4}
D. π6\dfrac{\pi }{6}
E. π8\dfrac{\pi }{8}

Explanation

Solution

We first use the triangle formula of the angles and then the trigonometric additional form of tan⁡−1x+tan⁡−1y=tan⁡−1x+y1−xy{{\tan }^{-1}}x+{{\tan }^{-1}}y={{\tan }^{-1}}\dfrac{x+y}{1-xy}. We also use Pythagoras’ theorem b2+c2=a2{{b}^{2}}+{{c}^{2}}={{a}^{2}}. We put the values of x=(ca+b),y=(ba+c)x=\left( \dfrac{c}{a+b} \right),y=\left( \dfrac{b}{a+c} \right) and find the particular solution for the inverse.

Complete step-by-step solution:
In ΔABC\Delta ABC, we get ∠A=90∘\angle A={{90}^{\circ }}. Therefore, ΔABC\Delta ABC is a right-angle triangle whose hypotenuse is the opposite side of the angle ∠A=90∘\angle A={{90}^{\circ }}.

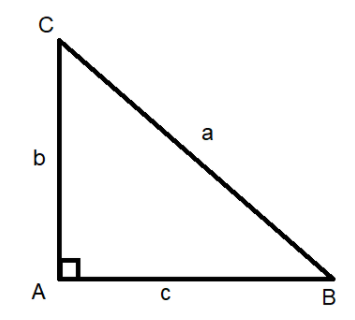
From Pythagoras’ theorem we know that b2+c2=a2{{b}^{2}}+{{c}^{2}}={{a}^{2}}.
We now use the trigonometric additional form of tan⁡−1x+tan⁡−1y=tan⁡−1x+y1−xy{{\tan }^{-1}}x+{{\tan }^{-1}}y={{\tan }^{-1}}\dfrac{x+y}{1-xy}.
Now we place x=(ca+b),y=(ba+c)x=\left( \dfrac{c}{a+b} \right),y=\left( \dfrac{b}{a+c} \right).
We get tan⁡−1(ca+b)+tan⁡−1(ba+c)=tan⁡−1(ca+b+ba+c1−ca+b×ba+c){{\tan }^{-1}}\left( \dfrac{c}{a+b} \right)+{{\tan }^{-1}}\left( \dfrac{b}{a+c} \right)={{\tan }^{-1}}\left( \dfrac{\dfrac{c}{a+b}+\dfrac{b}{a+c}}{1-\dfrac{c}{a+b}\times \dfrac{b}{a+c}} \right).
We multiply with (a+c)(a+b)\left( a+c \right)\left( a+b \right) and get

& {{\tan }^{-1}}\left( \dfrac{\dfrac{c}{a+b}+\dfrac{b}{a+c}}{1-\dfrac{c}{a+b}\times \dfrac{b}{a+c}} \right) \\\ & ={{\tan }^{-1}}\left( \dfrac{c\left( a+c \right)+b\left( a+b \right)}{\left( a+c \right)\left( a+b \right)-bc} \right) \\\ \end{aligned}$$ We simplify the equation and get $$\begin{aligned} & {{\tan }^{-1}}\left( \dfrac{c\left( a+c \right)+b\left( a+b \right)}{\left( a+c \right)\left( a+b \right)-bc} \right) \\\ & ={{\tan }^{-1}}\left( \dfrac{ac+{{c}^{2}}+{{b}^{2}}+ab}{{{a}^{2}}+ab+ac+bc-bc} \right) \\\ \end{aligned}$$ We replace the values ${{b}^{2}}+{{c}^{2}}={{a}^{2}}$ in the equation. $$\begin{aligned} & {{\tan }^{-1}}\left( \dfrac{ac+{{c}^{2}}+{{b}^{2}}+ab}{{{a}^{2}}+ab+ac+bc-bc} \right) \\\ & ={{\tan }^{-1}}\left( \dfrac{ac+{{a}^{2}}+ab}{ac+{{a}^{2}}+ab} \right) \\\ & ={{\tan }^{-1}}1 \\\ \end{aligned}$$ Now as the angle is an angle of a triangle, we can find the particular solution of the inverse. So, $${{\tan }^{-1}}\left( \dfrac{c}{a+b} \right)+{{\tan }^{-1}}\left( \dfrac{b}{a+c} \right)={{\tan }^{-1}}1=\dfrac{\pi }{4}$$. **Therefore, the correct option is C.** **Note:** Although for elementary knowledge the principal domain is enough to solve the problem. But if mentioned to find the general solution then the domain changes to $-\infty \le x\le \infty $. In that case we have to use the formula $x=n\dfrac{\pi }{2}+a$ for $\tan \left( x \right)=\tan a$ where $-\dfrac{\pi }{2}\le a\le \dfrac{\pi }{2}$. For our given problem $${{\tan }^{-1}}1=\dfrac{\pi }{4}$$, the general solution will be $x=n\dfrac{\pi }{2}+\dfrac{\pi }{4}$. Here $n\in \mathbb{Z}$. But for $\Delta ABC$, we get $\angle A={{90}^{\circ }}$. So, other angles are acute.