Question
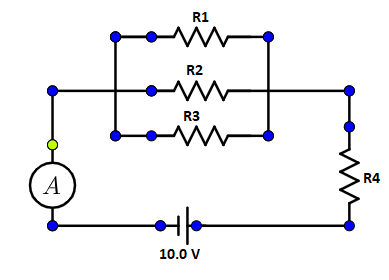
Question: If the ammeter in the circuit below reads \(5.0\,A\), the voltage drop across resistor \(1\) is \(3....
If the ammeter in the circuit below reads 5.0A, the voltage drop across resistor 1 is 3.0V. The resistance of the resistor 3 is 6.0Ω.
Which table most accurately represents other information we can know about quantities related to this circuit?
A)
| Current through Resistor 1 | Cannot determine |
|---|---|
| The voltage drop across resistor 2 | 3.0V |
| Current through resistor 3 | 0.50A |
| Power in resistor 4 | 35.0W |
B)
| Current through Resistor 1 | Cannot determine |
|---|---|
| The voltage drop across resistor 2 | 3.0V |
| Current through resistor 3 | 3.33A |
| Power in resistor 4 | Cannot determine |
C)
| Current through Resistor 1 | Cannot determine |
|---|---|
| The voltage drop across resistor 2 | 3.0V |
| Current through resistor 3 | 3.33A |
| Power in resistor 4 | Cannot determine |
D)
| Current through Resistor 1 | Cannot determine |
|---|---|
| The voltage drop across resistor 2 | 10.0V |
| Current through resistor 3 | 10.0A |
| Power in resistor 4 | Cannot determine |
E)
| Current through Resistor 1 | Cannot determine |
|---|---|
| The voltage drop across resistor 2 | 10.0V |
| Current through resistor 3 | Cannot determine |
| Power in resistor 4 | 35.0W |
Solution
The solution for this question is determined by using two formulas. One is Ohm’s law and another formula is Power in the circuit. By Ohm's law, the voltage drop across the resistor and the current through the resistor are determined, and then by using the power formula the power can be determined.
Formula used:
Ohm’s law gives the relation between the voltage, current, and resistance,
V=IR
Where V is the voltage in the circuit, I is the current in the circuit and R is the resistance in the circuit
Power in the circuit is given by,
P=VI
Where P is the power in the circuit, V is the voltage in the circuit and I is the current in the circuit.
Complete step by step answer:
Given that,
The current in the circuit, I=5.0A
The voltage drop across resistor 1 is, V1=3.0V.
The resistance of the resistor 3 is, R3=6.0Ω.
Voltage of the battery, V=10V
As the three resistance R1, R2 and R3 are connected in parallel, so the voltage drop across R1, R2 and R3 are same, then,
V1=V2=V3=3.0V.................(1)
Now, the current through the resistor 3 is,
By Ohm’s law,
⇒I3=R3V3
By substituting the voltage drop across resistor 3 and the resistance of the resistance 3 in the above equation, then
⇒I3=63
On dividing the above equation, then
⇒I3=0.5A...............(2)
The voltage drop across the resistor 4 is,
V4=V−V1
⇒V4=10−3
⇒V4=7V
Now, the power in resistor 4,
⇒P4=V4I4
By substituting the voltage drop across R4 and the current through the resistor 4 in the above equation, then
⇒P4=7×5
On multiplying the above equation, then
⇒P4=35W.................(3)
Hence, from equation (1), equation (2), and equation (3), we can say that option (A) is the correct answer.
Note:
Ohm’s law is the first important law that shows the relation between voltage, current, and resistance. The voltage 4 is determined by the difference of the voltages, the total voltage is 10V and the voltage drop across R1, R2 and R3 is 3.0V, then the voltage drop across resistor 4 is the difference of the total voltage and the voltage drop across the resistors.
