Question

If the acceleration of the cylinder of mass m and radius R and that of plank of mass M placed on smooth surface if pulled with a force F as shown in figure is $a = \dfrac{F}{{M + xm}}$, find the value of x. Given that sufficient friction is present between cylinder and the plank surface to prevent sliding of cylinder.

Answer 1

First, we have to draw the free body diagram of the given assembly and then resolve the forces acting on the assembly and resolve the acceleration. Expression of the acceleration is given in the question, so use Newton’s second law of motion and determine the value of the x.

Complete step by step answer:
The free body diagram of the assembly is,

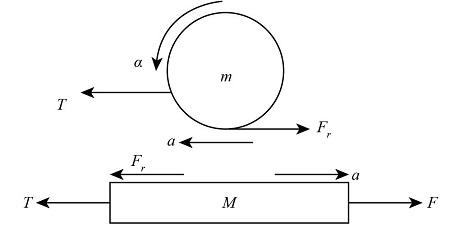
In the above diagram, it is clear that on the cylinder and plank various forces are acting in different directions and direction of accelerations are also different. So, resolve the forces and acceleration for the determination of x.
First we will resolve the forces that are acting on the cylinder of mass m with the help of Newton’s law, therefore we get
$T - {f_r} = ma$…… (1)
Here, $T$ is the tension force, ${f_r}$ is the friction force between cylinder and plank, $a$ is the linear acceleration and $m$ is the mass of the cylinder.
Now we will resolve the forces that are acting on the plank of mass M with the help of Newton’s law; therefore, we get
$F - T - {f_r} = Ma$……. (2)
Here $F$ is the force applied on the plank and $M$ is the mass of the plank.
The cylinder acquires linear acceleration as well as tangential acceleration, The formula we can use for the tangential acceleration is ${a_t} = r\alpha$, so we will resolve the accelerations also, therefore we get,
$R\alpha - a = a\\\ \implies R\alpha = 2a$……. (3)
Here $R$ is the radius of the cylinder and $\alpha$ is the angular acceleration of the cylinder.
The expression of the torque is,
$\tau = {f_f}R$…… (4)
But we know the another expression of the torque, that is
$\tau = I\alpha$...... (5)
We will use the equation (4) and (5) for the calculation of frictional force, so
${f_f}R = I\alpha$
By using the moment of inertia $I = \dfrac{1}{2}m{R^2}$ in the above equation, we get
${f_f}R = \left( {\dfrac{1}{2}m{R^2}} \right)\alpha \\\ {f_f} = \dfrac{{mR\alpha }}{2}$
Substitute the value from equation (3) in the above equation.
${f_f} = \dfrac{{m\left( {2a} \right)}}{2}\\\ \implies {f_r} = ma$........................... (6)
From equation (1), (2) and (7), we can obtain the required value of x.
Therefore, we get
$F - T - {f_r} = Ma\\\ \implies F - \left( {ma + {f_r}} \right) - {f_r} = Ma\\\ \implies F - ma - 2{f_r} = Ma\\\ \implies F - ma - 2\left( {ma} \right) = Ma$

On further solving the above equation, we get
$F - 3ma = Ma\\\ \implies F = \left( {M + 3m} \right)a\\\ \implies a = \dfrac{F}{{\left( {M + 3m} \right)}}$

Therefore, the value of x is 3.

Note:
The direction of the frictional force acting on the cylinder and plank will be the opposite. Also, give the correct direction to the various forces and acceleration in the free body diagram because they are used to resolve forces. The wrong directions of forces may lead to an incorrect answer.