Question

If the acceleration due to gravity at the surface of the earth is g, the work done in slowly lifting the body of mass m from earth’s surface to a height R equal to the radius of the earth is:
A. $\dfrac{mgR}{2}$
B. $mgR$
C. $mgR$
D. $mg\dfrac{R}{4}$

Answer 1

We know that work done is given by the difference in potential energies at two different points vertically. We will be using, to calculate the work done for our given situation. Before that, we need to determine the acceleration due to gravity at the given height h equal to radius of earth R from earth’s surface.

Formula Used:
$g=\dfrac{GM}{{{R}^{2}}}$
$W=-(mg{{h}_{2}}-mg'{{h}_{1}})$
Where,
${{h}_{1}}$ = radius of earth R
${{h}_{2}}$ = The distance from centre of earth to the highest point given 2R

Complete step by step answer:
We know that acceleration due to gravity at earth’s surface is given by g.
Therefore, we need to find the acceleration due to gravity at the given height.

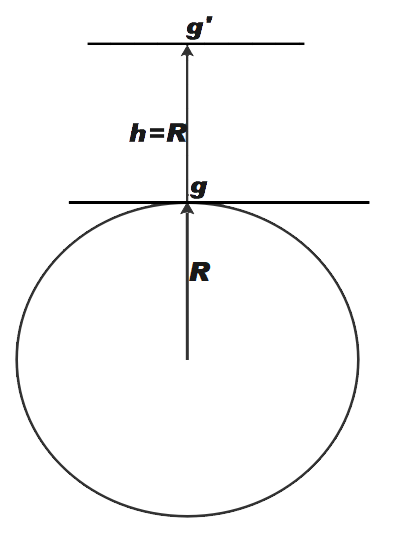
We know,
$g=\dfrac{GM}{{{R}^{2}}}$
So let’s say acceleration due to gravity at height h = 2R is given by g’
Therefore,
$g'=\dfrac{GM}{{{\left( 2R \right)}^{2}}}$ ……………………. (since h = 2R)
$g'=\dfrac{GM}{4{{R}^{2}}}$
$\therefore g'=\dfrac{g}{4}$ …………. (1)
Now using the formula for work done
We get,
$W=-(mg{{h}_{2}}-mg'{{h}_{1}})$
Substituting the given values and g’ from (1)
We get,
$W=-(mgR-m\dfrac{g}{4}2R)$
After solving the above equation
We get,
$W=\dfrac{1}{2}mgh$
Therefore, the correct answer is option D.

Note:
We can solve the given question by considering the earth's centre point as datum plane and using the energy conservation formula
$W=\Delta K.E+\Delta P.E$
Since there is no kinetic energy it is taken as zero
Therefore,
$\Delta P.E=(mgh-0)$since the energy at datum plane is always taken as zero
$\Delta P.E=m\dfrac{g}{4}\times 2R$
$\Delta P.E=\dfrac{1}{2}mgR$
So, we get the same result using this method.