Question

If the 11 letters A, B , . . . . K arbitrary permutation of the integers (1, 2, . . ., 11) then (A-1) (B-2) (C-3) . . . (K-11) will be
(a). Necessarily zero
(b). Always odd
(c). Always even
(d). None of them

Answer 1

- Hint: The 11 letter denotes 11 integers. Part A,B,C,…,K as 2,3,4,…,1 and find if their product is zero, odd or even. Now put A,B,C,….,K as 3,4,5,….,1,2 and find their product. Compare the cases and if it is odd, even or zero.

Complete step-by-step solution -

We have been given 11 letters from the alphabets as.
A, B, C, D, E, F, G, H, K
Now these 11 letters denote an arbitrary permutation of the integers.
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11
Thus we can write it as,

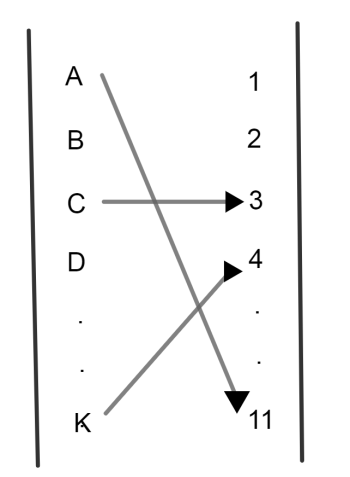
These 11 letters can denote any arbitrary permutation of the integers.
Thus for, (A-1) (B-2) (C-3) . . . (K-11) (1)
Let us first put A = 2, B = 3, C = 4 . . . . K = 11, as we only have been given 11 integers. Thus (1) becomes
(A-1) (B-2) (C-3) . . . . . . (K-11)
= (2-1) (3-2) (4-3) . . . . . (1-11) = 1x1x1x . . . . . . x (-10) = -10
Thus we got an even number.
Now let us put A = 3, B = 4, C = 5 . . . . I = 1, K = 2.
Thus (1) becomes,
(A-1) (B-2) . . . . (I-10) (K-11) = (3-1) (4-2) . . . . (1-10) (2-11)
= 2 x 2 x . . . . (-9) x (-9)
=$2^9$x$(-9)^2$=$2^9$x$9^2$

From the above $2^9$ is an even no. and $9^2$ is an odd number. The multiplication of an even and odd no is always even.
Thus, we got an even number.
Hence from these we can say (A-1) (B-2) (C-3) . . . (K-11) will always be even.
Option (c) is the correct answer.

Note: In the given set of nos. {1,2,3, ,11} out of which 5 numbers are even and the rest 6 are odd. Thus there is at least one factor involving subtraction of an odd no. from another odd no. So at least one of the factors is even. This product is always even.