Question

If tangents are drawn to the ellipse ${{x}^{2}}+2{{y}^{2}}=2$ at all points on the ellipse other than its four vertices, then the midpoints of the tangents intercepted between the coordinate axes lie on the curve:
(a) $\dfrac{{{x}^{2}}}{2}+\dfrac{{{y}^{2}}}{4}=1$,
(b) $\dfrac{{{x}^{2}}}{4}+\dfrac{{{y}^{2}}}{2}=1$,
(c) $\dfrac{1}{2{{x}^{2}}}+\dfrac{1}{4{{y}^{2}}}=1$,
(d) $\dfrac{1}{4{{x}^{2}}}+\dfrac{1}{2{{y}^{2}}}=1$.

Answer 1

We start solving the problem by converting the given equation of tangent into the standard form $\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$ to find the value of a and b. We then find the parametric equation to represent the point on the ellipse. We then find the general equation of the tangent of the ellipse using this parametric point. We then find the x and y-intercepts and then find the midpoint of them. We then equate it to $\left( x,y \right)$ and use the identity ${{\sin }^{2}}\theta +{{\cos }^{2}}\theta =1$ to get the required locus.

Complete step by step answer:
We have given that the tangents are drawn at all points except the four vertices for the ellipse ${{x}^{2}}+2{{y}^{2}}=2$. We need to find the locus of the midpoints of the tangents intercepted between the coordinate axes.

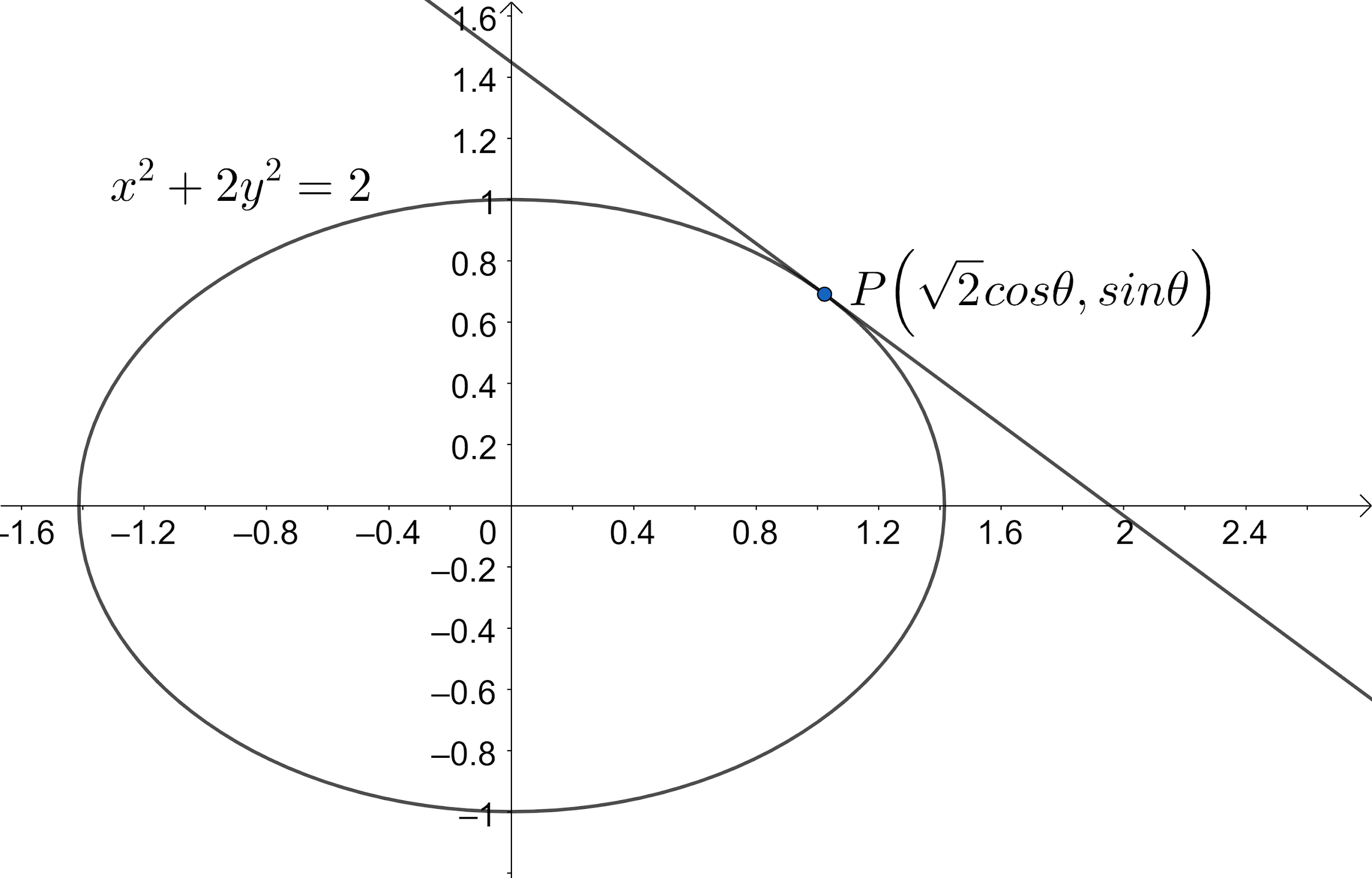
Let us convert the given equation of tangent into the standard form $\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$.
So, we have got the equation of the ellipse as ${{x}^{2}}+2{{y}^{2}}=2$.
$\Rightarrow \dfrac{{{x}^{2}}}{2}+\dfrac{2{{y}^{2}}}{2}=1$.
$\Rightarrow \dfrac{{{x}^{2}}}{2}+\dfrac{{{y}^{2}}}{1}=1$.
$\Rightarrow \dfrac{{{x}^{2}}}{{{\left( \sqrt{2} \right)}^{2}}}+\dfrac{{{y}^{2}}}{{{1}^{2}}}=1$. Comparing with the standard form we get $a=\sqrt{2}$ and $b=1$.
We know that the parametric point on the ellipse is $\left( a\cos \theta ,b\sin \theta \right)$. Using this we get the parametric point as $\left( \sqrt{2}\cos \theta ,\sin \theta \right)$.
We know that the general form of the equation of the tangent to ellipse is $\dfrac{x\cos \theta }{a}+\dfrac{y\sin \theta }{b}=1$. Using this we get the equation of the tangent to the ellipse ${{x}^{2}}+2{{y}^{2}}=2$ as $\dfrac{x\cos \theta }{\sqrt{2}}+\dfrac{y\sin \theta }{1}=1$.
$\Rightarrow \dfrac{x}{\sqrt{2}\sec \theta }+\dfrac{y}{\operatorname{cosec}\theta }=1$ ---(1).
We know that the intercept form of the equation of the line is defined as $\dfrac{x}{a}+\dfrac{y}{b}=1$, where a is x intercept and b is y intercept and the points on x and y axes where the line intercepted is $\left( a,0 \right)$ and $\left( 0,b \right)$. Comparing this with equation (1) we get x-intercept as $\sqrt{2}\sec \theta$ and y-intercept as $\operatorname{cosec}\theta$ and the points $A\left( \sqrt{2}\sec \theta ,0 \right)$ and $B\left( 0,\operatorname{cosec}\theta \right)$.
Let us assume the mid-point of A and B be $\left( x,y \right)$.
So, we have $\left( x,y \right)=\left( \dfrac{\sqrt{2}\sec \theta +0}{2},\dfrac{0+\operatorname{cosec}\theta }{2} \right)$.
$\Rightarrow \left( x,y \right)=\left( \dfrac{\sqrt{2}\sec \theta }{2},\dfrac{\operatorname{cosec}\theta }{2} \right)$.
$\Rightarrow \left( x,y \right)=\left( \dfrac{1}{\sqrt{2}\cos \theta },\dfrac{1}{2\sin \theta } \right)$.
Equating corresponding coordinates on both sides, we get
$\Rightarrow x=\dfrac{1}{\sqrt{2}\cos \theta }$ and $y=\dfrac{1}{2\sin \theta }$.
$\Rightarrow \cos \theta =\dfrac{1}{\sqrt{2}x}$ and $\sin \theta =\dfrac{1}{2y}$.
We know that ${{\sin }^{2}}\theta +{{\cos }^{2}}\theta =1$.
$\Rightarrow {{\left( \dfrac{1}{\sqrt{2}x} \right)}^{2}}+{{\left( \dfrac{1}{2y} \right)}^{2}}=1$.
$\Rightarrow \dfrac{1}{2{{x}^{2}}}+\dfrac{1}{4{{y}^{2}}}=1$.
We have found locus of the mid points of the all tangents as $\dfrac{1}{2{{x}^{2}}}+\dfrac{1}{4{{y}^{2}}}=1$.
∴ The midpoints of the tangents intercepted between the coordinate axes lie on the curve $\dfrac{1}{2{{x}^{2}}}+\dfrac{1}{4{{y}^{2}}}=1$.

So, the correct answer is “Option C”.

Note: Whenever we have this type of problem, we first solve all in general form and then equate it to variables to x and y to represent the equation of the curve. We can also find the equation of the tangent by finding the slope of tangent using differentiation at the parametric point. If we are unable to remember the parametric point, then take the equivalent point that satisfies the equation of the ellipse in first place. We can have similar problems related to hyperbola.