Question
Question: If tangent and normal to a rectangular hyperbola xy = c<sup>2</sup> cut off intercepts a<sub>1</sub>...
If tangent and normal to a rectangular hyperbola xy = c2 cut off intercepts a1 and a2 on one axis and b1, b2 on the other, then:
A
a1 = b1
B
a2 = b2
C
a2a1=b2b1
D
a1a2 + b1b2 = 0
Answer
a1a2 + b1b2 = 0
Explanation
Solution
Tangents and normals are at 900. Product of slopes is -1.
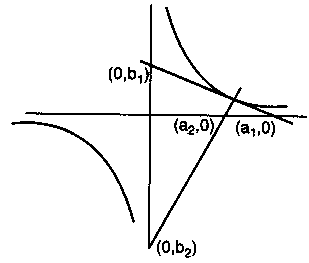
(−a1b1)(−a2b2)=−1
a1a2 + b1b2 = 0
