Question

If $\tan (x) = \dfrac{5}{{12}}$ in the third quadrant then find other trigonometric ratios?

Answer 1

Hint : Here in this question, we have to find the value of all six trigonometric ratios i.e., sin, cos, sec, cosec and cot using a given value of tan ratio. This can be solved by using a definition of trigonometric ratios, trigonometric identities and by applying a ASTC rule of trigonometry we get the required values of all six trigonometric ratios.

Complete step-by-step answer :
Trigonometric functions are real functions which relate an angle of a right-angled triangle to ratios of two side lengths.
There are six trigonometric ratios, sine, cosine, tangent, cosecant, secant and cotangent which can be abbreviated as sin, cos, tan, cosec, sec and cot.
Consider the given question:
$\Rightarrow \tan (x) = \dfrac{5}{{12}}$ ----------(1)
given that the angle $x$ lies in the third quadrant.
In the third quadrant, $\tan x$ and $\cot x$ are positive and all other ratios are negative.

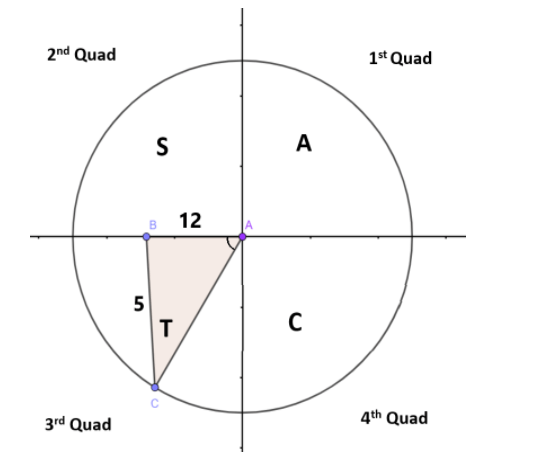
By the definition of trigonometry, Cotangent is a reciprocal of tangent ratio i.e.,
$\Rightarrow \cot x = \dfrac{1}{{\tan x}}$
Substitute the value of $\tan \left( x \right)$ from equation (1), then
$\Rightarrow \cot \left( x \right) = \dfrac{1}{{\left( {\dfrac{5}{{12}}} \right)}}$
$\Rightarrow \cot \left( x \right) = \dfrac{{12}}{5}$ -------(2)
Now consider, the trigonometric identity $cose{c^2}x = 1 + {\cot ^2}x$ , then
$\Rightarrow cosec(x) = \sqrt {1 + co{t^2}x}$
Substitute the value of $cot\left( x \right)$ from equation (2), then
$\Rightarrow cosec(x) = \sqrt {1 + {{\left( {\dfrac{{12}}{5}} \right)}^2}}$
$\Rightarrow cosec(x) = \sqrt {1 + \dfrac{{144}}{{25}}}$
Take 25 as LCM in RHS , then
$\Rightarrow cosec(x) = \sqrt {\dfrac{{25 + 144}}{{25}}}$
$\Rightarrow cosec(x) = \sqrt {\dfrac{{169}}{{25}}}$
As we know 169 is a square number of 13 i.e., $169 = {13^2}$ and 25 is a square number of 5 i.e., $25 = {5^2}$ , then we have
$\Rightarrow cosec(x) = \sqrt {\dfrac{{{{13}^2}}}{{{5^2}}}}$
$\Rightarrow cosec(x) = \sqrt {{{\left( {\dfrac{{13}}{5}} \right)}^2}}$
In third quadrant cosecant are negative, then
$\Rightarrow cosec(x) = - \dfrac{{13}}{5}$ -------(3)
By the definition, trigonometric ratio sine is a reciprocal of cosecant i.e., $\sin x = \dfrac{1}{{cosec(x)}}$
substitute value of $cosec\left( x \right)$ from equation (3), then
$\Rightarrow \sin \left( x \right) = \dfrac{1}{{\left( { - \dfrac{{13}}{5}} \right)}}$
$\Rightarrow \sin \left( x \right) = - \dfrac{5}{{13}}$ -------(4)
Now consider, the trigonometric identity ${\cos ^2}x + {\sin ^2}x = 1$ , then
$\Rightarrow \cos (x) = \sqrt {1 - {{\sin }^2}x}$
Substitute the value $\sin \left( x \right)$ from equation (4), then
$\Rightarrow \cos (x) = \sqrt {1 - {{\left( { - \dfrac{5}{{13}}} \right)}^2}}$
$\Rightarrow \cos (x) = \sqrt {1 - \dfrac{{25}}{{169}}}$
Take 169 as LCM in RHS, then
$\Rightarrow \cos (x) = \sqrt {\dfrac{{169 - 25}}{{169}}}$
$\Rightarrow \cos (x) = \sqrt {\dfrac{{144}}{{169}}}$
As we know 169 is a square number of 13 i.e., $169 = {13^2}$ and 25 is a square number of 5 i.e., $144 = {12^2}$ , then we have
$\Rightarrow cos(x) = \sqrt {\dfrac{{{{12}^2}}}{{{{13}^2}}}}$
$\Rightarrow cos(x) = \sqrt {{{\left( {\dfrac{{12}}{{13}}} \right)}^2}}$
In third quadrant cosine are negative, then
$\Rightarrow cos(x) = - \dfrac{{12}}{{13}}$ -------(5)
By the definition, trigonometric ratio secant is a reciprocal of cosine i.e., $\sec \left( x \right) = \dfrac{1}{{cos(x)}}$
substitute value of $cos\left( x \right)$ from equation (5), then
$\Rightarrow \sec \left( x \right) = \dfrac{1}{{\left( { - \dfrac{{12}}{{13}}} \right)}}$
$\Rightarrow \sec \left( x \right) = - \dfrac{{13}}{{12}}$ -------(6)
Therefore, the values of all six trigonometric ratios are
$\sin \left( x \right) = - \dfrac{5}{{13}}$ , $cos(x) = - \dfrac{{12}}{{13}}$ , $\tan (x) = \dfrac{5}{{12}}$ , $\sec \left( x \right) = - \dfrac{{13}}{{12}}$ , $cosec(x) = - \dfrac{{13}}{5}$ and $\cot \left( x \right) = \dfrac{{12}}{5}$ .

Note : ASTC rule says all trigonometric functions are positive in the first quadrant (sin, cos, tan and its reciprocals). sin and cos functions are positive in the second quadrant, all other function sides are negative. tan and cot functions are positive in the third quadrant and all other functions are negative. Finally in fourth quadrant cos and sec functions are positive and all other functions are negative.