Question

If $\tan x = \dfrac{{ - 4}}{3},$x in quadrant II. Find the value of $\sin \dfrac{x}{2},\cos \dfrac{x}{2},\tan \dfrac{x}{2}$

Answer 1

Here we will find the hypotenuse side by using Pythagoras theorem and will use the trigonometric identities and place the values in it and simplify the fractions along with that applying the All STC rules.

Complete step-by-step answer:
Given that the function $\tan x = \dfrac{{ - 4}}{3},$ x lies in the second quadrant.
$\Rightarrow \dfrac{\pi }{2} < x < \pi$
Also, in the second quadrant sine is positive and cosine is negative by All STC rule.
We know the tangent angle in any right angled triangle is the ratio of the opposite side to the adjacent side.

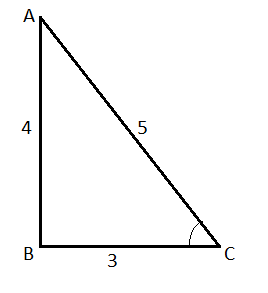
Above right angled triangle implies that –
$AB = 4 \\\ BC = 3 \\\$
By using the Pythagoras theorem – hypotenuse square is equal to the sum of the square of the opposite side and the square of the adjacent side.
$\Rightarrow AC = \sqrt {A{B^2} + B{C^2}}$
Place the values in the above equation –
$\Rightarrow AC = \sqrt {{4^2} + {3^2}}$
Simplify the above equation –
$\Rightarrow AC = \sqrt {16 + 9} \\\ \Rightarrow AC = \sqrt {25} \\\$
Take square-root on the right hand side of the equation –
$\Rightarrow AC = 5$
By All STC rules, sine is positive and cosine is negative.
Now, we know that the sine function is the ratio of the opposite side to the hypotenuse side.
$\sin x = \dfrac{{AB}}{{AC}} = \dfrac{4}{5}$
Similarly, Cosine function is the ratio of the adjacent side to the hypotenuse.
$\cos x = \dfrac{{BC}}{{AC}} = - \dfrac{3}{5}$
As, given that –
$\dfrac{\pi }{2} < x < \pi$ for “x” lies in the second quadrant.
$\Rightarrow \dfrac{\pi }{4} < \dfrac{x}{2} < \dfrac{\pi }{2}$for $\dfrac{x}{2}$ lies in the first quadrant.
Now, use the identity –
$1 - \cos x = 2{\sin ^2}\dfrac{x}{2} \\\ \Rightarrow \sin \dfrac{x}{2} = \pm \sqrt {\dfrac{{1 - \cos x}}{2}} \\\$
Place the values in the above equation-
$\Rightarrow \sin \dfrac{x}{2} = \pm \sqrt {\dfrac{{1 - \left( {\dfrac{{ - 3}}{5}} \right)}}{2}}$
Simplify the above equation –
$\Rightarrow \sin \dfrac{x}{2} = \pm \sqrt {\dfrac{8}{{10}}} \\\ \Rightarrow \sin \dfrac{x}{2} = \pm \dfrac{2}{{\sqrt 5 }} \\\$
Since the above angle is in the first quadrant.
$\therefore \sin \dfrac{x}{2} = \dfrac{2}{{\sqrt 5 }}{\text{ }}....{\text{ (A)}}$
Now, use the identity –
$1 + \cos x = 2co{\operatorname{s} ^2}\dfrac{x}{2} \\\ \Rightarrow \cos \dfrac{x}{2} = \pm \sqrt {\dfrac{{1 + \cos x}}{2}} \\\$
Place the values in the above equation-
$\Rightarrow \cos \dfrac{x}{2} = \pm \sqrt {\dfrac{{1 + \left( {\dfrac{{ - 3}}{5}} \right)}}{2}}$
Simplify the above equation –
$\Rightarrow \cos \dfrac{x}{2} = \pm \sqrt {\dfrac{2}{{10}}} \\\ \Rightarrow \cos \dfrac{x}{2} = \pm \dfrac{1}{{\sqrt 5 }} \\\$
Since the above angle is in the first quadrant, cosine is positive
$\therefore \cos \dfrac{x}{2} = \dfrac{1}{{\sqrt 5 }}{\text{ }}....{\text{ (B)}}$
Now, use identity –
$\tan \dfrac{x}{2} = \dfrac{{\sin \dfrac{x}{2}}}{{\cos \dfrac{x}{2}}}$
Place values in the above equation-
$\tan \dfrac{x}{2} = \dfrac{{\dfrac{2}{{\sqrt 5 }}}}{{\dfrac{1}{{\sqrt 5 }}}}$
Like and same terms from the denominator and the numerator cancel each other.
$\Rightarrow \tan \dfrac{x}{2} = 2{\text{ }}....{\text{ (C)}}$

Note: Remember the All STC rule, it is also known as ASTC rule in geometry. It states that all the trigonometric ratios in the first quadrant ($0^\circ \;{\text{to 90}}^\circ$ ) are positive, sine and cosec are positive in the second quadrant ($90^\circ {\text{ to 180}}^\circ$ ), tan and cot are positive in the third quadrant ($180^\circ \;{\text{to 270}}^\circ$ ) and sin and cosec are positive in the fourth quadrant ($270^\circ {\text{ to 360}}^\circ$ ).